Revised: 2022/2/25、3/16、10/7
ln-ln plot 和 log-log plot 是很多科學數據的呈現方式,以下以實例說明 ln-ln plot 和 log-log plot 之斜率特色。
表格中 x、y 數據可近似成 y = 0.1096x +11.111
(y vs. x 圖的斜率 0.1096)
Fig. 1
表格中 ln(x)、ln(y) 數據可近似成 ln(y) = 0.6901ln(x) + 0.088
故 ln(y) vs. ln(x) 圖的斜率 0.6901
Fig. 2
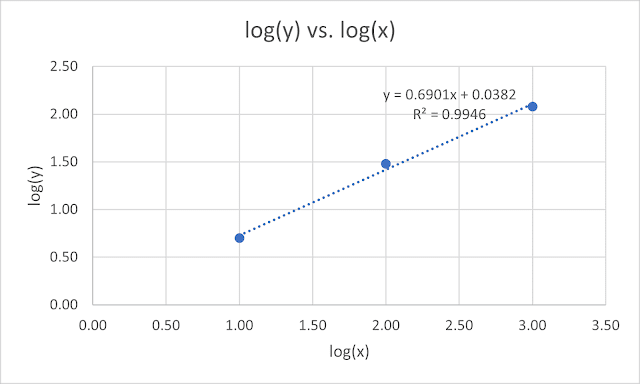
表格中 log(x)、log(y) 數據可近似成 log(y) = 0.6901log(x) + 0.0382
故 log(y) vs. log(x) 圖的斜率 0.6901,與 Fig. 2 斜率相同
Fig. 3
一、x 值乘以常數 3

表格中 ln(3x)、ln(y) 數據可近似成 ln(y) = 0.6901ln(3x) - 0.6702 (等同 ln(y) = 0.06901ln(x) + 0.088)
故 ln(y) vs. ln(3x) 圖的斜率 0.6901,與 Fig. 2 斜率相同
[註:dln(y)/dln(3x) = dln(y)/(dln(3) + dln(x)) = C,整理可得 dln(y)/dln(x) = C,Figs. 2、4 斜率均為 C]
Fig. 4
表格中 log(3x)、log(y) 數據可近似成 log(y) = 0.6901log(3x) - 0.2911 (等同 log(y) = 0.6901log(x) + 0.0382)
故 log(y) vs. log(3x) 圖的斜率 0.6901,與 Fig. 2 斜率相同
Fig. 5二、x 值乘以常數 3,且 y 值乘以常數 4
表格中 ln(3x)、ln(4y) 數據可近似成 ln(4y) = 0.6901ln(3x) + 0.7161 (等同 ln(y) = 0.6901ln(x) + 0.088)
故 ln(4y) vs. ln(3x) 圖的斜率 0.6901,與 Fig. 2 斜率相同
Fig. 6
表格中 log(3x)、log(4y) 數據可近似成 log(4y) = 0.6901log(3x) + 0.311 (等同 log(y) = 0.6901log(x) + 0.0382)
故 ln(4y) vs. ln(3x) 圖的斜率 0.6901,與 Fig. 2 斜率相同
Fig. 7
三、結論
(1) 對於同樣的數據,ln-ln 作圖 與 log-log 作圖的斜率相同 (Fig. 2 vs. Fig. 3)。
(2) ln-ln 作圖 與 log-log 作圖的斜率,不因 x、y 值乘以常數後而改變斜率 (Fig. 2 vs. Fig. 4 vs. Fig. 6 或 Fig. 3 vs. Fig. 5 vs. Fig. 7)。
[補充]
今有 Y vs. X 數據如下,試比較下方兩種繪圖 (1) ln(Y) vs. X、(2) log(Y) vs. X。
<解>
隨著 X 值增加,曲線均呈單調遞增且開口朝上。但是在固定 X 值下,第二種作圖 (藍色) 的斜率值較較小。
X Y
0 367636765.2
2 488429357.9
4 653706842
6 881634852.7
8 1198537506
10 1642901534
12 2271516966
14 3168988571
16 4462621430
18 6345968764
20 9116501378
22 13236572214
24 19433283712
26 28864159422
28 43395617491
30 66077516211
32 1.01963E+11
34 1.5955E+11
36 2.53344E+11
38 4.08508E+11
40 6.69432E+11
42 1.11581E+12
44 1.89337E+12
46 3.27389E+12
48 5.77451E+12
50 1.04008E+13
52 1.91531E+13
54 3.61058E+13
56 6.97721E+13
58 1.38419E+14
60 2.82368E+14
62 5.9333E+14
64 1.28663E+15
66 2.88524E+15
68 6.70568E+15
70 1.61918E+16
72 4.0728E+16
74 1.07028E+17
76 2.94778E+17
78 8.53904E+17
80 2.61168E+18









沒有留言:
張貼留言