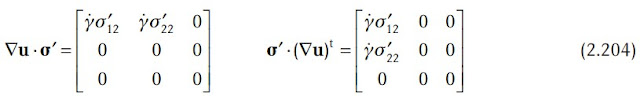考慮在 x-y 平面,一個具 x 方向均勻剪切之穩態恆溫流動,速度場為 u(γ̇ y, 0, 0),流體具 Maxwell 行為,其黏度為 η、鬆弛時間為 λ。
(b) 推導 Maxwell model 的 extra-stress tensor 的各項,以及三個測黏函數 (viscometric functions):σ12 = τ(γ̇ )、σ11 - σ22 = N1(γ̇ )、σ22 - σ33 = N2(γ̇ )。在什麼情況下 Maxwell 流體的行為接近牛頓流體?
(c) 計算 arbitrary pressure p'、流體靜力壓力 p (hydrostatic pressure)。
對流的項為 (下標 1、2、3 代表 x、y、z)<解>
(a) 速度場梯度張量 (velocity field gradient tensor)、其它轉置 (transpose) 分別為
因為流動是穩態、均勻的,σ' 的物質導數為零因此,upper convected derivative 為
[註:Johnson 和 Segalman (1977) 修正 Maxwell model,引入張量 σ' 的 covariant 和 contravariant derivatives

因為 σ = - p'I + σ',可得
我們找到了一個正值的第一正向應力差,和一個等於零的第二正向應力差。當第一正向力差 N1(γ̇ ) (= σ11 - σ22) 相較於剪切應力可忽略時,也就是對應很小的 Weissenberg number,Maxwell 流體的行為如牛頓流體。
我們找到了一個正值的第一正向應力差,和一個等於零的第二正向應力差。當第一正向力差 N1(γ̇ ) (= σ11 - σ22) 相較於剪切應力可忽略時,也就是對應很小的 Weissenberg number,Maxwell 流體的行為如牛頓流體。
(c) 流體靜力壓力 p 為