由於動量是一個向量,所以平衡式中的每一項都必須是一個向量。我們使用單位向量 u1 和 u2 來表示平面 1 和 2 處的流動方向。然後動量守恆可寫成
這裡,Ptot = ∫ρvdV 是系統中的總動量 (total momentum)。該等式說明,系統內的總動量因動量對流進、出系統而改變 (the convection of momentum),也包括作用在系統上的各種力:壓力在系統兩端的力 (pressure forces)、固體表面作用在系統中流體的力 (the force of the solid surfaces)、以及作用在系統中壁內流體的重力 (the force of gravity)。下標 “s→f” 用於提醒力的方向。
透過引入質量流率的符號和符號 △,我們最終得到非穩態巨觀動量平衡 (unsteady-state macroscopic momentum balance)
如果系統中的總動量不隨時間變化,那麼我們得到穩態巨觀動量平衡 (steady-state macroscopic momentum balance)
我們再次強調這是一個向量方程式 (vector equation)。它對於計算流體作用於固體表面上的力 Ff→s 相當有用,例如作用於彎管 (pipe bend) 或渦輪葉片 (turbine blade) 的力。 事實上,我們已經在 Eq. 6.1-3 中使用了上述方程式的簡化版本。
關於紊流 (turbulent flow) 的注意事項:(i) 對於紊流,通常將 <v> 替換為 <v−>、<v2> 替換為 <v− 2>;在後者中,我們忽略了通常很小的項 <v'2 −> (相較於 <v− 2>)。(ii) 然後我們進一步將 <v− 2>/<v−> 替換為 <v−>,這樣做的誤差很小;對於 Eq. 5.1-4 的經驗 1/7 冪次律速度曲線,<v− 2>/<v−> = 50<v−>/49,如此的誤差在 2% 左右。(iii) 當我們做出這個假設時,我們通常會刪除尖括號 (angular brackets) 和橫線 (overbars) 以簡化符號。也就是說,我們會讓 <v1−> ≡ v1、<v1− 2> ≡ v12,平面 2 的量也進行類似的簡化。
Reference: RB Bird, WE Stewart, EN Lightfoot, Transport Phenomena, 2nd ed (Wiley 2002).


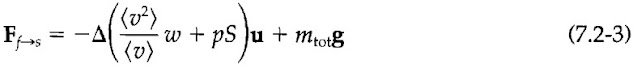
沒有留言:
張貼留言