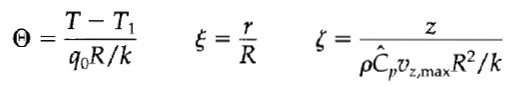§10.8 強制對流 (Forced Convection)

於前面的幾節中，我們主要強調固體的熱傳導問題 (heat conduction in solids)，在本節和接下來的小節，我們將探討兩種流體的熱輸送型式 (heat transport in fluids)，分別為 (i) 強制對流 (forced convection) 和 (ii) 自然對流 (free convection or natural convection)。這兩種對流模式的主要差異可見 Fig. 10.8-1。大部分工業熱傳問題通常屬於兩者中的其一，然而，在有些問題中，這兩種效應都必需被考慮，稱之為混合對流 (mixed convection)。

Figure 10.8-1 非恆溫系統的強制對流與自然對流之比較

本文將探討圓管中 (circular tube) 之強制對流，由於系統夠簡單所以具有解析解。假設黏滯流體的物理性質 (μ, k, ρ, C_p^{^}) 為定值且在半徑 R 的圓管中形成層流 (laminar)。於 z < 0，流體的溫度是均勻的並維持在入口溫度 T₁ (uniform at the inlet temperature)；於 z > 0，有一個固定的徑向熱通量 q_r = -q₀ 於管壁。這樣的系統實際存在於一個被電加熱線圈 (electrical heating coil) 均勻包覆的管子，則 q₀ 為正，如果管子正在被冷卻，則 q₀ 必需為負值。

如 Fig. 10.8-1 所述，求解強制對流之熱傳問題的第一步為計算系統的流速分佈 (velocity profiles)。藉由對管流進行殼均衡方法 (shell balance method) 所得到的速度分佈為 v_r = 0、v_θ = 0 以及 (見 §2.3)

(10.8-1)

當自入口往下的距離遠大於入口距離時 (entrance length)，Eq. 10.8-1 的抛物線分佈 (parabolic distribution) 將是有效的。

Figure 10.8-2

在這個問題中，熱在 r 和 z 的方向被傳遞，因此，對於能量平衡我們使用墊圈形狀系統 (washer-shaped system)，此墊圈是由厚度 △r 的環狀區域與厚度 △z 的平板相交所形成 (見 Fig. 10.8-2)。在這個問題中，我們處理的是一個流動流體，因此合併能量通量向量 e (combined energy flux vector) 的所有項都將被保留，在能量平衡式中的各種貢獻分別如下

(10.8-2, 3, 4, 5, 6)

最後一個貢獻 (10.8-6) 是重力作功於環內液體的變化率，也就是單位體積的力 ρg_z 乘上體積 2πr△r△z，再乘上流體向下的速度 v_z。能量的平衡可以透過加總這些貢獻並令其為零，再接著除以 2π△r△z 可得到

(10.8-7)

當 △r 和 △z 趨近於零，可以得到

(10.8-8)

因為重力向量作用在 +z 方向，所以 g_z 的下標 z 已被忽略 。

接著我們使用 Eqs. 9.8-6 和 9.8-8 寫下合併能量通量向量的 r 和 z 分量之表示式，並且利用已知的事實，即 v 向量的非零分量為軸向分量 v_z

(10.8-9, 10)

將這些通量表示式代入 Eq. 10.8-8 並已知 v_z 僅是 r 方向的函數，經整理後可得

(10.8-11)

上式的第二個中括號為零 (運動方程式的 z 分量；Eq. 3.6-4)。+μ(∂v_z/∂r)² 是黏滯加熱 (viscous heating)，但我們在此忽略之。第一個中括號的最後一項有關於軸向的熱傳導，因為我們從經驗知道相較於軸向熱對流，它通常很小，也將被忽略。因此，我們將求解的式子為

(10.8-12)

此偏微分方程式 (partial differential equation) 經求解後，將描述流體溫度是 r 和 z 的函數。其邊界條件為

(10.8-13, 14, 15)

我們接著將此問題轉換成無因次的形式 (dimensionless form)，無因次量的選擇可以是任意的，這裡我們選擇

(10.8-16, 17, 18)

一般來說，我們試著選取適當的無因次量，使最後的問題算式具有最少的參數。在此問題，ξ = r/R 是很自然的選擇，因為 r/R 已經出現在微分方程式 (10.8-12)；無因次溫度的選擇是因為第二和第三個邊界條件。當確認這兩個無因次變數後，無因次軸座標也很自然決定了。

最後，無因次形式的問題算式變成

(10.8-19)

其邊界條件為

(10.8-20, 21, 22)

此偏微分方程式 (10.8-19) 結合這些邊界條件已被解出，但這裡我們並沒有提供完整的解答。

然而，若是能得到 ζ 值很大的漸近解 (asymptotic solution)，將會非常具啟發性，這是因為當流體足夠遠離一開始的加熱段，我們預期管壁的固定熱通量將造成流體溫度的上升並與 ζ 呈線性。我們也預期溫度曲線的形狀 (是 ξ 的函數) 將隨著 ζ  的增加，而不再有進一步的變化 (只有向上平移)，見 Fig. 10.8-3。因此，當 ζ 值很大時，下方形式的解是合理的

(10.8-23)

其中，C₀ 是接下來要決定的常數。

Figure 10.8-3

Equation 10.8-23 很明顯不是這個問題的完全解答 (complete solution)，它雖允許偏微分方程式和邊界條件一和二被滿足，但並不滿足邊界條件三。因此，我們將後者取代為一個積分條件 (見 Fig. 10.8-4)

(10.8-24)

或者無因次的形式

(10.8-25)

這個條件表示在一段距離為 ζ，透過管壁進入管中的能量等於，在位置 ζ 通過截面離開的能量和在 ζ = 0 進入的能量差。

將假定的函數 Eq. 10.8-23 代入 Eq. 10.8-19 得到下方 Ψ 的常微分方程式 (見 Eq. C.1-11)

(10.8-26)

這個方程式可以對 ξ 積分兩次並將結果代至 Eq. 10.8-23 可得

(10.8-27)

三個常數可由 B.C.s 1, 2, 4 決定。

(10.8-28, 29, 30)

將這些值代入 Eq. 10.8-27 可得

(10.8-31)

此結果透露，無因次溫度是無因次徑向和軸向座標的函數，當 ζ → ∞，Eq. 10.8-31 為精確解 (exact solution)；當 ζ > 0.1，預測準度在 2% 內。

一但溫度分佈已知，我們可以得到各種衍生的物理量。有兩種常用的平均溫度被用來與固定 ρ 與 C_p^{^} 的流動流體連結

(10.8-32, 33)

Erratum (Eq. 10.8-32): reads 7/24 → should read 1/8 

兩個平均溫度都是 z 的函數。<T> 是在位置 z 的截面之算術平均溫度 (arithmetic average temperature)；T_b 是整體溫度 (bulk temperature)，也就是在位置 z 切斷管子，並收集向前噴出的流體於容器中，並徹底混合，這種平均溫度有時稱為杯混合溫度 (cup-mixing temperature) 或流動平衡溫度 (flow-average temperature)。

我們接著估算局部熱傳驅動力 T₀ -T_b，這是在距離 z，壁溫和整體溫度具有的差值

(10.8-34)

其中，D 是管徑。我們可以重排這個結果成為一個無因次管壁熱通量

(10.8-35)

其在第 14 章被識別為 Nusselt number。

在我們結束這節之前，我們指出前面介紹的無因次軸向座標 ζ 可重寫成

(10.8-36)

這裡 D 是管徑、Re 是 Reynolds number (用於本書 Part I)、Pr 和 Pé 分別為 Prandtl 和 Péclet numbers (已於第 9 章介紹)。我們將在第 11 章發現 Re 和 Pr 被預期在強制對流問題出現，這個點將在第 14 章強化並與熱傳係數的關聯進行連結。

Reference: RB Bird, WE Stewart, EN Lightfoot, Transport Phenomena, 2nd ed (Wiley 2002).

Visual Studio 2019

早期學習撰寫程式，需自費買程式開發工具，例如，Compaq Visual Fortran 6.6。然而，近年來，編譯器變為免費，例如，微軟 Microsoft 提供 Visual Studio 2019 功能完善的整合式開發環境供個人免費使用 (integrated development environment, IDE)，實為使用者一大福音 。

書籍 - The Structure and Rheology of Complex Fluids

這是一本由著名流變學家 Ronald G. Larson，針對複雜流體 (complex fluids) 所寫的專書。書中將各式各樣的流體分為三大類，包括高分子溶液、膠體懸浮液、液晶。這書對於時常接觸複雜流體的人是相當有用的參考書籍。

書名: The Structure and Rheology of Complex Fluids
作者: Ronald G. Larson
出版社: Oxford University Press
版本: 1998 年

Table of Contents

PART I FUNDAMENTALS

Chapter 1 Introduction to Complex Fluids

Chapter 2 Basic Forces

PART II POLYMERS, GLASSY LIQUIDS, AND POLYMER GELS

Chapter 3 Polymers

Chapter 4 Glassy Liquids

Chapter 5 Polymer Gels

PART III SUSPENSIONS

Chapter 6 Particulate Suspensions

Chapter 7 Particulate Gels

Chapter 8 Electro- and Magnetoresponsive Suspensions

Chapter 9 Foams, Emulsions, and Blends

PART IV LIQUID CRYSTALS AND SELF-ASSEMBLING FLUIDS

Chapter 10 Liquid Crystals

Chapter 11 Liquid-Crystalline Polymers

Chapter 12 Surfactant Solutions

Chapter 13 Block Copolymers

向列型液晶高分子之流動性質 (Flow Properties of Nematic LCPs)

本文主要探論主鏈向列型液晶高分子 (main-chain nematic liquid crystalline polymers) 的流變性質，向列型 LCP 的流動性質非常特別，因此尚未被全然了解；此外，不同的 LCP 間的差異性也頗大，即便是單一 LCP 流體，其在不同剪切率區間的行為也大不相同。雖然 LCP 的流變行為具有一定的複雜性，但它仍然具有一些典型的特色，以下將一一介紹。

1. 黏度之濃度及溫度相依性 (Dependence of Viscosity on Concentration and Temperature)

當液晶高分子自均向過渡至向列型狀態 (isotropic-nematic transition)，將伴隨著剪切黏度的下降；見 Figs. 11.4a (濃度效應) 和 11.5 (溫度效應)。這個結果並不意外，因為在向列型狀態，分子間彼此的滑動比起在均向狀態更加容易，所以造成黏度下降。因此，當我們增加系統濃度 (Fig. 11.4) 或降低系統溫度 (Fig. 11.5)，可以從均向狀態轉變至向列型狀態，造成黏度下降；很明顯，這趨勢與一般系統所觀察到的結果相反 (一般而言，增加濃度或降低溫度將造成黏度增加)。所以，當碰到均向過渡至向列型狀態時，常伴隨著上述易被觀察到之流變異常 (rheological anomaly)；話雖如此，我們仍應同時透過偏光顯微鏡 (polarizing microscope)，謹慎確認是否真有此過渡狀態行為之發生。

Figure 11.4 濃度效應

Figure 11.5 溫度效應

2. 區間 I 之剪切致稀 (Region I Shear Thinning)

Onogi 和 Asada 提出的三區間流動曲線 (three-region flow curve) 可以用來描述主鏈型 LCP 的黏度對剪切率之行為。在 Fig 11.6，區間 II 是牛頓平台區 (Newtonian plateau)，而區間 I 和 III 分別為低剪切率 (low-shear-rate) 和高剪切率 (high-shear-rate) 的剪切致稀區間 (shear thinning regions)。Figure 11.7 是 hydroxypropylcellulose (HPC) 水溶液的三區間流動曲線；Fig. 11.8 是 poly(1,4-phenylene-2,6-benzobisthiazole) (PBZT；也稱為 PBT) 於 methane sulfonic acid 的三區間流動曲線 (唯空心符號對應到完全向列型流體 (fully nematic liquids))；Fig. 11.9 是 PBLG 於 m-cresol 的三區間流動曲線 (臨界濃度為 37%)；Fig. 11.10 是熱致型 Vectra A LCP 的三區間流動曲線。

對於可撓性 (flexible) 或剛性 (rigid) 高分子的均向性溶液 (isotropic solutions)，類比於區間 II 和 III 的行為是常見的。例如於 Fig. 11.8 的均向 PBZT 溶液 (實心符號) 具有一個低剪切率的牛頓區間 (或區間 II) 和一個高剪切率的剪切致稀區間 (或區間 III)，但是沒有區間 I 的存在。對於處於均向狀態的向列型高分子溶液，其在牛頓區間 (區間 II) 的分子方向性分佈不太受到流場的擾動，但是在高剪切率的剪切致稀區間則不然 (區間 III)。

我們可以說，相較於一般的均向性液體，LCP 溶液最大的特色是具有低剪切率的剪切致稀區間 (區間 I)，這是因為 LCP 流體具有液晶特色所致 (liquid-crystalline character) 。 不過，區間 I 的剪切致稀並不是出現於所有 LCP 流體，事實上，沒有區間 I 的例子遠較有的例子來得多，而且因為力矩解析度的儀器限制，流變儀在極低剪切率的數據是比較不可靠的 (例如，見 Fig. 11.8)，然而，從理論的觀點來看，區間 I 的存在是有可能的。

Figure 11.6 三區間流動曲線

Figure 11.7

Figure 11.8

Figure 11.9

Figure 11.10

3. 負值之第一正向應力差 (Negative First Normal Stress Differences)

對於有些向列型 LCP，另一個特殊的性質是在一段剪切率範圍間的穩態第一正向應力差 N₁ 為負值。Figure 11.12 呈現 PBLG 溶液之 N₁ 和黏度 η 對剪切率的作圖，我們可以發現 N₁ 兩次的變號，N₁ 在最低剪切率範圍是正的，接著在中間剪切率是負的，最後在最高剪切率再次變為正值。然而，對有些 LCP，N₁ 恆為正值，但我們也無法排除它們在更高的剪切率會變成負值 (實驗範圍以外)。對於具負值 N₁ 且實驗數據較無爭議的例子，負值 N₁ 所對應的剪切率範圍接近區間 III 的開始 (onset of Region III)，因此，如果 LCP 到了區間 III 仍無負值 N₁，我們幾乎可以斷定它在所有區間都不會有負值 N₁，例如 Fig. 11.13。此外，在穩態剪切流的起動實驗，即便最終穩態的 N₁ 為正值，我們仍可觀察到暫態過程中 N₁ 為負值的情況 (transient negative N₁) 。

Figure 11.12

Figure 11.13

4. 暫態剪切應力 (Transient Shear Stresses)

對於 LCP，當剪切流場起動後，複雜的暫態剪切應力行為時常被觀察到，例如應力隨時間具多重過衝和下衝 (multiple overshoots and undershoots)，一般而言，需經過至少 50-100 應變單位才能達到穩態。在區間 II，特徵黏彈響應時間 (characteristic viscoelastic response times) 與剪切率成反比，因此，當我們以剪切率乘上時間做為 x 軸 (即應變)，並將暫態的應力對時間之曲線重新繪製，便可得到一條單一的重疊曲線，而且這種尺度化 (scaling) 往往非常精準。例如，Figure 11.14 呈現 PBLG 溶液無因次化後的應力 (normalized stress) 對應變之作圖，即便兩個剪切率差到 50 倍 (0.1 vs. 5.0 1/s)，曲線仍重疊相當好 (請注意，這是討論的是一個達穩態後，再突然施加的反方向剪切實驗 (sudden reversal in the direction of shearing))。這個實驗疊合的結果再次透露，最大應力響應值之間 (between maxima in the stress response) 的時間週期 P 與剪切率呈反比。因為類似的多重應力過衝行為也可以在滾翻的小分子向列型液晶發現 (tumbling small-molecular nematics)，所以我們可以說 PBLG 溶液屬於滾翻 (tumbling) 而不是流動定向型 (flow-aligning type)。

Figure 11.14

Reference: RG Larson, The Structure and Rheology of Complex Fluids (Oxford University Press 1999).

液晶高分子之分子特色 (Molecular Characteristic of Liquid-Crystalline Polymers)

液晶高分子 (liquid-crystalline polymer, LCP) 因為其鏈勁度 (chain stiffness) 和高度的分子方向性 (high molecular orientation)，所以具有相當特別的整體性質 (bulk properties) 和加工性 (processabiity)。固化的 LCP 纖維 (fiber) 具有數十到數百 GPa (gigapascals) 的拉伸模數 (tensile modulus)，或 1-4 GPa 的破裂強度 (fracture strengths)。如 Fig. 2-1 所示，液晶相 (liquid crystal phase) 是介於結晶態 (crystalline state) 與液態 (liquid state) 之間的中間相 (mesophase)。

LCP 材料具有良好的抗溶劑腐蝕 (solvent attack)、抗溼度侵害 (moisture attack)、抗熱膨脹 (thermal expansion)、抗軟化 (softening)、抗分解 (decomposition) 等性質；此外，LCP 的良好加工性來自於它們在向列型熔體態 (nematic melt state) 具有之低黏度。因此，LCP 的商業化產品甚廣，包括防彈背心的纖維 (fibers for bulletproof vests)、電子和光學原件的封裝 (packaging for electrical and optical components)、輕量化且強韌的飛機零件 (strong, lightweight aircraft parts) 等。而熱致型液晶高分子 (thermotropic LCPs) 常見於射出成型，主要是因為 LCP 的低收縮量 (low shrinkage)、低射壓和夾壓 (injection and clamping pressures；因為低熔體黏度)、快速週期時間 (fast cycle times；因為高熱傳導率和低熔解熱) 等優點。

能夠形成液晶溶液或熔體 (liquid-crystalline solutions or melts) 的高分子大多為半剛性 (semirigid) 或包含剛性單元 (rigid units；或稱液晶分子基 (mesogens))，於液晶態，分子 (或者至少液晶分子基) 的方向性分佈是非均向的 (anisotropic orientation distributions)。如 Fig. 11.1 所示，對於主鏈 (main-chain) 型 LCPs，剛性單元位在主鏈上；對於側鏈型 (side-chain) LCPs，則透過可撓性分隔段 (flexible spacers) 將剛性單元接在主鏈上。

Figure 11.1 不同剛性程度的高分子

對於單一成份的材料，或者熱致型 (thermotropic) LCPs，液晶態 (liquid-crystalline state) 可透過自結晶態 (crystalline state) 開始增加溫度，或者自均向態 (isotropic state) 降低溫度；反觀，對於溶致型 (lyotropic) LCPs，加入溶劑可以變化液態結晶度 (liquid crystallinity)。正如同小分子，單一種類的高分子在不同的溫度或濃度下也可表現出多液晶相 (multiple-liquid crystalline phases)，例如向列型 (nematic)、層列型 (smectic) 或圓柱型 (columnar)；見 Fig. 1。

(a)

(b)
Figure 1 (a) 向列型 (nematic)、(b) 層列型 (smectic) [from Wikipedia]

幾種具代表性的主鏈型 LCPs 可見於 Fig. 11.2，這幾種高分子不論在剛性或形成向列型液晶相 (或其它液晶相) 的情況都很不相同。我們知道能否形成向列型的狀態主要是受控於軸比 b_K/d (axial ratio)，其中 b_K 是 Kuhn 長度 (等於兩倍的 persistence 長度 λ_p)，d 是分子的等效直徑。一般而言，剛性越大的分子越傾向生成液晶相而不是均向性的相。不過，剛性也同時會促進結晶性 (crystallinity)，因此當宣稱一個為液晶狀態的系統時，結晶的行為應該儘量被抑制發生。

Figure 11.2 一些常被研究的 LCPs 之化學結構，前四種常用做溶致高分子，最後兩種則是熱致高分子

對於主鏈型 LCPs，分子的可撓度將沿著主鏈均勻地分佈，例如 Fig. 11.2 的 PBLG、HPC 或 Vectra A。又或者可集中於可撓性的分隔段，例如 OQO(phenylsulfonyl)10。前者稱為持續可撓分子 (persistently flexible molecules)，常以蟲形鏈 (worm-like chain) 模擬之；後者則可以使用自由連結鏈 (freely-jointed chain) 合理地模擬之；見 Fig. 11.3。

Figure 11.3 蟲形高分子和 Kuhn 鏈

Reference: RG Larson, The Structure and Rheology of Complex Fluids (Oxford University Press 1999).

簡單步進剪切形變之應力張量 (Stress Tensor in a Simple Step-Shear Deformation)

於時間 t = T_eq 時，應力張量為 (stress tensor)

(1)

透過 Eq. 1，我們可以計算 t = T_eq 之模數 (其為形變 E 的函數)。在，Eq. 1 涉及鏈滑動機制 (chain-slippage mechanism) 中的兩種效應: (i) 鏈段分佈 (segmental distribution) 沿著原始鏈 (primitive chain) 之平衡過程；(ii) 纏結點 (number of entanglement strands) 的減少。第一個效應與 Eq. 1 中的第一個 <...> 內的 |E∙u| 有關，第二個效應與 <|E∙u|>^-1 有關。對於一個簡單的步進剪切形變 (simple step-shear deformation)，E 為

(2)

應力張量的 xy 分量可由 Eq. 1 得到

(3)

其中，u_x、u_y、u_z 是單位向量 u 在 x、y、z 方向的分量。為了從 Eq. 3 計算不同施加應變 λ 對應的剪切力 T_xy，我們變換至球面座標 (r, θ, 𝜙) (spherical coordinates):

(4)

並對所有的方向 (all orientations) 進行平均的運算 <...>，即

(5)

以下附上推導 Eq. 3 所需的運算過程

(6)

Reference: YH Lin, Polymer Viscoelasticity: Basics, Molecular Theories and Experiments (World Scientific 2003).