 |
| Figure 1.2 |
A. 高分子和高分子凝膠 (Polymer Solutions and Polymer Gels)
Figure 3.1 圖示比較高分子的流體狀態 (fluid state),例如溶液,和彈性狀態 (elastic state),例如凝膠。高分子溶液屬於流體狀態,長鏈高分子彼此纏結形成黏滯材料,雖然其流動受阻,但仍會流動。的確,只要時間夠長,容器內的高分子溶液可以被倒至桌面。反觀,交聯的 (cross-linked) 高分子凝膠具有大的分子網狀結構 (molecular network),因此無法流動也無法被倒出。如果將容器倒置 (upside down),凝膠將掉出但是不會在桌面上攤平。簡單來說,流體可以無限制地被形變 (deformed indefinitely),而彈性材料在有限的形變下是可逆的 (reversibly deformed to a finite extent)。
B. 黏度和彈性 (Viscosity and Elasticity)
不論材料是流體還是彈性材料,均可透過 Fig. 3.2a 的實驗裝置進行研究。樣品被置於兩平行平板間,下板固定而上板水平移動並被一條線拉住。假設時間 t = 0,一個重量物質被懸吊於此線,然後於稍後的時間 t = t0,這條線被剪斷。這樣的操作,可於時間 0 和 t0 間,施加一個固定的力 F 於上板。材料的機械性質可以用上板的位移行為 d(t) 表徵,如果材料是流體,只要施力存在,上板將持續移動,且當施力移除後,仍與起始位置保有一定的位移。反觀,如果材料是彈性體,上板將移動至機械平衡的位置,且當施力移除後,上板將回到起始位置。
為了分析結果,我們定義兩個量,剪切應力 σ 和剪切應變 γ。剪切應力 σ 是作用於樣品表面每單位面積的剪切力 (shearing force)。如 Fig. 3.2a 的幾何,則 σ 為
其中,S 是材料的上半部表面面積。剪切應變 γ 為
其中,h 是兩板間距。如果材料是均勻的 (uniform),σ 和 γ 的關係將與樣品大小無關。
如果材料是理想彈性材料 (ideal elastic material or Hookean elastic),應力將正比於應變,即
其中,G 是材料常數 (material constant),稱為剪切模數 G (shear modulus)。對於這樣的理想材料,剪切應變 γ(t) 的響應如 Fig. 3.2b 的虛線所示
當 t > t0,γ(t) = 常數
對於高分子材料,γ(t) 將更加複雜,如 Figs. 3.2b 和 3.2c 的實線所示。高分子材料通常具有很長的鬆弛時間 (long relaxation times),且在達到穩態之前表現出複雜的暫態行為,材料之複雜時間相依行為是所謂的黏彈性 (viscoelasticity)。
 |
| Figure 3.2a |
為了分析結果,我們定義兩個量,剪切應力 σ 和剪切應變 γ。剪切應力 σ 是作用於樣品表面每單位面積的剪切力 (shearing force)。如 Fig. 3.2a 的幾何,則 σ 為
其中,S 是材料的上半部表面面積。剪切應變 γ 為
其中,h 是兩板間距。如果材料是均勻的 (uniform),σ 和 γ 的關係將與樣品大小無關。
如果材料是理想彈性材料 (ideal elastic material or Hookean elastic),應力將正比於應變,即
其中,G 是材料常數 (material constant),稱為剪切模數 G (shear modulus)。對於這樣的理想材料,剪切應變 γ(t) 的響應如 Fig. 3.2b 的虛線所示
當 t < t0,γ(t) = σ/G = 常數
當 t > t0,γ(t) = 0
反觀,如果材料是理想黏滯流體 (ideal viscous fluid or Newtonian fluid),剪切應力將正比於剪切應變的時間導數 γ̇ (time derivative of the shear strain),即
其中,η 是另一個材料常數,稱為黏度 (或剪切黏度)。對於這樣的材料,應變的響應如 Fig. 3.2c 的虛線所示
當 t < t0,γ(t) = (σ/η)t當 t > t0,γ(t) = 常數
C. 彈性係數 (Elastic Constants)
如果彈性材料所受的形變很小,應力與應變的關係是線性的,且材料的機械性質可完全由彈性常數 (elastic constants) 所表徵。對於均向性材料 (isotropic materials),其具有兩個彈性常數,一個是剪切模數 G (Eq. 3),另一個是體積彈性係數 K (bulk modulus),將於下方介紹。
假設一個材料被額外的壓力 △P 均向地壓縮 (compressed isotropically),造成體積由 V 變成 V + △V (如果 △P > 0 則 △V < 0;見 Fig. 3.3a)。如果體積的變化很小,則 △P 將正比於比值 △V/V (體積應變;volume strain),可寫成
其中,K 是體積彈性係數 (為正值)。在 Eq. 5 中的定義,負號的加入使 K 值為正。對於其它種類形變的材料彈性係數,可由 K 和 G 表之。假設一個矩形材料在 z 方向均勻地被拉伸 (stretched uniformly),見 Fig. 3.3c。拉伸比例為 λ (elongational ratio),即 λ = Lz'/Lz (其中,Lz、Lz' 是形變前、後材料在 z 方向的長度)。拉伸應變 𝛜 (elongational strain) 可定義成
假設一個材料被額外的壓力 △P 均向地壓縮 (compressed isotropically),造成體積由 V 變成 V + △V (如果 △P > 0 則 △V < 0;見 Fig. 3.3a)。如果體積的變化很小,則 △P 將正比於比值 △V/V (體積應變;volume strain),可寫成
其中,K 是體積彈性係數 (為正值)。在 Eq. 5 中的定義,負號的加入使 K 值為正。對於其它種類形變的材料彈性係數,可由 K 和 G 表之。假設一個矩形材料在 z 方向均勻地被拉伸 (stretched uniformly),見 Fig. 3.3c。拉伸比例為 λ (elongational ratio),即 λ = Lz'/Lz (其中,Lz、Lz' 是形變前、後材料在 z 方向的長度)。拉伸應變 𝛜 (elongational strain) 可定義成
經證明,楊氏模數可以用 G 和 K 表之
如果材料是沿著 z 方向被拉伸,它將在 x 和 y 方向收縮,在 x 方向的應變被定義為 𝛜x = Lx'/Lx - 1,而帕松比 υ (Poisson's ratio) 則被定義成
υ 可以用 G 和 K 表之
如果材料是沿著 z 方向被拉伸,它將在 x 和 y 方向收縮,在 x 方向的應變被定義為 𝛜x = Lx'/Lx - 1,而帕松比 υ (Poisson's ratio) 則被定義成
υ 可以用 G 和 K 表之
體積彈性係數 K 代表一個被均向壓縮材料之回復力,可定義於流體和彈性材料。K 的大小主要是由材料的密度所決定,而且其值不會因流體轉變成彈性材料後有太大的改變,例如,橡膠和高分子熔體的 K 大約在 1 GPa,與金屬的值相近。
在另一方面,剪切模數 G 代表一個變形的材料回復至原來形狀之力,這種力不存在於流體,但卻存在於彈性材料。當高分子流體具有交聯 (cross-links),剪切模數開始不為零且隨交聯反應增加。
值得注意的是,軟物質之所以具有柔軟度 (softness) 是因為剪切模數小,但前面已經提到,軟物質的體積彈性係數約和金屬的值差不多,且遠大於剪切模數。因此,當討論軟物質的形變時,我們可以假設 K 是無限大,也就是體積的改變並不會在在材料受外力變形的情況下發生,這個假設稱為不可壓縮假設 (incompressible assumption),在一般的應力範圍內 (< 10 MPa),這個假設對於軟物質在流體和彈性狀態是合理的。對於不可壓縮材料,Eq. 8 可近似成
 |
| Figure 3.3 |
D. 彈性材料之連續體力學 (Continuum Mechanics for Elastic Materials)
D.1. 形變自由能密度 (Free Energy Density of Deformation)
我們接下來討論彈性材料如何受外力而變形。只要系統處於平衡 (equilibrium),材料的機械行為完全由一個形變自由能 (deformation free energy) 函數所表徵。為了定義之,我們選擇一個材料在所有外力被移除 (external forces removed) 的平衡狀態 (equilibrium state) ,並定義此狀態為參考狀態 (reference state)。我們接著定義形變狀態 (deformed state) 與參考狀態之自由能差值為形變自由能。在參考狀態每單位體積的形變自由能稱為形變自由能密度 (deformation free energy density)。
在討論形變自由能的明確表示式之前,我們先詳細說明材料的形變。
 |
| Figure 3.4 |
D.2. 正交形變 (Orthogonal Deformation)
最剪單的形變例子是正交形變,如 Fig. 3.4a 所示,一個立方體的材料沿著三個正交的方向被拉伸 λ1、λ2、λ3 倍,造成原來在 (rx, ry, rz) 的點位移至新的位置
最剪單的形變例子是正交形變,如 Fig. 3.4a 所示,一個立方體的材料沿著三個正交的方向被拉伸 λ1、λ2、λ3 倍,造成原來在 (rx, ry, rz) 的點位移至新的位置
若讓 f(λ1, λ2, λ3) 為此形變對應的形變自由能密度 (簡化成 f(λi)),對於均向材料,如要計算材料受外力的形變,f(λi) 是我們唯一必需知道的量。
D.3. 均勻形變 (Uniform Deformation)
E 是常數張量 (constant tensor)。因為材料所有的體積單元 (volume elements) 以同樣的方式形變 (deformed in the same way),所以稱為均勻形變。如果以希臘字母當下標 α, β, γ 表示向量和張量的 x, y, z 分量,並採用 Einstein 表示法 (Einstein notation),則 Eq. 13 可寫成
Equation 14 中的 E 稱為形變梯度張量 (deformation gradient tensor),因為 E 可以寫成
形變 E 所對應的自由能變化量 f(E) 可以用 f(λi) 來表示。
D.4. 通用形變 (General Deformation)
通用形變所對應的形變自由能可以從 f(E) 計算得到。如 Fig. 3.4c 所示,任何的形變可表示成 r → r' = r'(r),屬非線性的對應 (nonlinear mapping),然而,局部的形變 (local deformation) 總是均勻的,因為一個小向量 drα (small vector) 總是對應到 drα' = (∂rα'/∂rβ)drβ (例如,在分量 x,drx' = (∂rx'/∂rx)drx + (∂rx'/∂ry)dry + (∂rx'/∂rz)drz)。在點 r 的形變梯度張量為 Eαβ(r) = ∂rα'/∂rβ (Eq. 15),因此,形變自由能之總和為 (total free energy of deformation)
我們透過適當的邊界條件可以讓 Ftot 最小化,得到材料的平衡狀態 (equilibrium state)。
平衡狀態亦可透過考慮材料的力平衡 (force balance) 取得。這個方法較為通用的原因是因為它可以解釋黏滯應力 (viscous stress),反觀,黏滯應力無法從自由能引伸出來。
Reference: M Doi, Soft Matter Physics (Oxford University Press 2013).






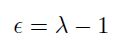










沒有留言:
張貼留言