辛普森雙重積分 (Simpson's Double Integral)

The algorithm above is to approximate an integral over a region that is not a rectangular one. It is straightforward to apply the algorithm to a special case, i.e., a rectangular region, by setting c(x) and d(x) equal to constants c and d, respectively (i.e., I = ∫_a^b∫_c^d f(x, y) dydx).

Example: ∫_1.4^2.0∫_1.0^1.5 ln(x + 2y) dydx ≈ 0.42955。

Reference: RL Burden, DJ Faires, AM Burden, Numerical Analysis, 10th ed (Cengage Learning 2016).

Pearson 等人提出之鏈拉伸模型 (Chain-Stretching Model of Pearson et al.)

本文介紹 Pearson 等人 [Pearson et al. (1989)] 提出的鏈拉伸模型 (chain-stretching model of Pearson et al.)，此模型是完整 Doi-Edwards-Marrucci-Grizzute (DEMG) 模型之簡化版本 (toy version)。Pearson 等人的模型包含了三個成份: 方向性張量 S、描述鏈拉伸的純量 λ、應力張量 σ (由 S 和 λ 表之)，這些方程式為 

於 Eq. 1，m(t, t') = (1/τ_d)exp(-(t-t')/τ_d) 是記憶函數 (memory function)，能補捉黏彈流體受應變後的應力鬆弛。Equation 1 的 Q(E(t, t')) 是形變相依的通用 Doi-Edwards 張量 (deformation-dependent "universal" tensor of Doi and Edwards)，其被形變梯度歷史 E(t, t') 定義成

(4)

此模型對起動剪切流場 (start of shear flow)、穩態剪切流場 (steady shear flow) 之基本預測分別呈現於 Fig. 1 和 Fig. 2。

(a) 無因次暫態黏度

(b) 鏈拉伸比值 λ
Figure 1 起動剪切流場之流變性質 (τ_d / τ_s = 50) 

(a) 無因次剪切應力、黏度

(b) 方向性張量 S 的 xy 分量

(c) 鏈拉伸比值 λ
Figure 2 穩態剪切流場之流變性質 (τ_d / τ_s = 50) 

Reference: 
1. DS Pearson, AD Kiss, LJ Fetters, M Doi, "Flow-induced birefringence of concentrated polyisoprene solutions," J Rheol 33, 517 (1989).
2. DW Mead, RG Larson, M Doi, "A molecular theory for fast flows of entangled polymers," Macromolecules 31, 7895 (1998).
3. TCB McLeish, "Tube theory of entangled polymer dynamics," Adv. Phys. 51, 1379 (2002).

方向分佈函數與向列相之有序參數 (Orientational Distribution Function & Order Parameter for Nematics)

方向分佈函數 (Orientational Distribution Function)

為了區別向列相 (nematic phase) 和均向相 (isotropic phase)，讓我們考慮分子方向性的分佈 (distribution of molecular orientation)。若我們以單位向量 u 代表分子的長軸方向；見 Fig. 5.1(a)。在均向相，u 均均分佈於一個單位球 |u| = 1 (unit sphere)；在向列相，u 在球的分佈變成不均勻。讓 ψ(u) 為 u 在單位球的分佈函數，並且被歸一化為 (normalized)

(1)

其中，du 代表球 |u| = 1 的表面元素 (surface element)，並且這個積分是全部的表面。

在均向相，ψ(u) 為常數並與 u 無相依性，因此 [註: 單位球的面積為 4π]

(2)

另一方面，若在向列相，ψ(u) 將朝導向體 n 的方向定向 (oriented toward the direction of the director n)，故 ψ(u) 變成非均向。

向列相之有序參數 (Order Parameter for Nematics)

讓我們考慮一個參數來表徵向列相中的非均向性 ψ(u)。這個參數的明顯候選人是一階矩 <u_α> (α = x, y, z) (first moment)，其中，<∙∙∙> 代表分佈函數 ψ(u) 的平均，即

(3)

不過，對於如 Fig. 5.1(a) 的對稱橢球分子 (symmetric ellipsoidal molecules)，<u_α> 總是等於零，這是因為 u 和 -u 的狀態是相同的，因此 ψ(u) 有反轉對稱 ψ(u) = ψ(-u) (inversion symmetry)。

我們因此考慮二階矩 <u_αu_β > (second moment)，在均向相，

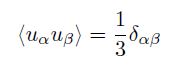(4)

[註: 在均向相，<u_x²> = <u_y²> = <u_z²>，且 <u_xu_y> = <u_yu_z> = <u_zu_x> = 0，因此，<u_αu_β> 可寫成 <u_αu_β> = Aδ_αβ 。因為 u_x² + u_y² + u_z² = 1，A = 1/3]

在另一方面，如果 u 完全朝向 n 排列，

(5)

 因此我們考慮以下這個參數

(6)

Q_αβ 為張量有序參數 (tensor order parameter)，其代表向列相的分子方向有序程度 (orientational order of the molecules)。對於均向相，Q_αβ = 0；對於向列相， Q_αβ ≠ 0。

如果 u 的分佈沿軸 n 具單軸對稱 (uniaxial symmetry)，Q_αβ 可寫成

(7)

其中，S 是代表分子沿 n 排列的程度，如果排列是完美的 (alignment is perfect)，則 S = 1；如果沒有排列 (no alignment)，則 S = 0。因此，S 也代表向列相之有序程度 (degree of the order)，稱為純量有序參數 (scalar order parameter)。為了避免與 S 混淆，Q_αβ 常被稱為張量有序參數 (tensor order parameter)。

張量有序參數 Q_αβ 包含兩種訊息，一個表示分子排列的程度，以純量有序參數 S 表之；另一個表示分子排列的方向，以導向體 n 表之。透過 Eq. 6

(8)

等式的右側等於 (2/3)S (透過 Eq. 7)。因此，S 可以表示成

(9)

其物理意義同前述。

Reference: M Doi, Soft Matter Physics (Oxford University Press 2013).

§1.7 對流動量輸送 (Convective Momentum Transport)

目前為止，我們已經討論分子動量輸送 (molecular transport of momentum)，並介紹一組量 π_ij，其代表通過垂直 i 方向表面之 j 方向動量通量。然後我們將 π_ij 和速度梯度和壓力進行關聯，並發現這個關係式涉及兩個材料參數 μ (viscosity) 和 κ (dilatational viscosity)。我們已於 §§1.4 和 1.5 了解黏度如何源自於分子在流體中的隨機運動 (random motion of the molecules)，也就是相對於流體整體運動的隨機分子運動。此外，在 Problem 1C.3 我們說明壓力對 π_ij 的貢獻來自於隨機分子運動。

事實上，動量也可以藉由流體的整體流動進行輸送，而此程序稱為對流輸送 (convective transport)。我們利用 Fig. 1.7-1 加以討論並聚焦在空間中，流體流經的一個正立方體形狀 (cube-shaped) 之區域，在正立方體的中心 (座標在 x, y, z)，流體的速度向量是 v。正如同在 §1.2 我們考慮通過點 x, y, z 的三個相互垂直平面 (陰影平面)，並了解有多少動量流過每一個平面，每個面具有單位面積 (unit area)。

通過 Fig. 1.7-1(a) 的陰影單位面積之體積流率為 v_x，此流體每單位體積帶有動量 ρv，因此，通過陰影面積的動量通量是 v_xρv，特別注意這是自較小 x 的區域 (less x) 往較大 x 的區域 (greater x) 傳遞之動量通量，同樣地，通過 Fig. 1.7-1(b) 的陰影面積之動量通量為 v_yρv，Fig. 1.7-1(c) 為 v_zρv。

這三個向量 ρv_xv、ρv_yv、ρv_zv 描述通過三個面積垂直個自軸之動量通量，這裡三個向量中的每一個向量均有其 x、y、z 分量。這些分量已整理在 Table 1.7-1 的對流動量通量分量 (convective momentum flux components)，ρv_xv_y 這個量是 y 動量通過表面垂直 x 方向之對流通量，它可與 τ_xy 這個量比較 (τ_xy 是 y 動量通過表面垂直 x 方向之分子通量)，此兩種輸送模式的符號規定 (sign convention) 是相同的。

收集 Table 1.7-1 的九個純量分量可以表示成

(1.7-1)

因為每個 ρvv 的分量有兩個下標，而個自對應一個座標方向，所以 ρvv 是一個二階張量 (second-order tensor)，稱為對流動量通量張量 (convective momentum-flux tensor)。Table 1.7-1 的對流動量通量張量之分量應該與 Table 1.2-1 的分子動量通量張量 (molecular momentum-flux tensor) 之分量相互比較。

接下來，我們想知道通過單位法向量 n 的表面元素之對流動量通量；見 Fig. 1.7-2。如果流體以速度 v 流過表面 dS，則自負的那側 (minus side) 流向正的那側 (plus side) 且通過表面的體積流率為 (n∙v)dS。因此，通過表面的動量流率為 (n∙v)ρvdS，對流動量通量為 (n∙v)ρv。根據附錄 A 的向量張量符號規則，也可寫成 n∙ρvv，也就是，單位法向量 n 和對流動量通量張量 ρvv 的內積。如果我們讓 n 接續為指向 x, y, z 方向的單位向量 (即 δ_x, δ_y, δ_z)，我們可以得到 Table 1.7-1 第二列 (欄) 的矩陣元素。
[例如: δ_x∙(Σ_jδ_xδ_jρv_xv_j) = Σ_jδ_jρv_xv_j = ρv_xv、δ_y∙(Σ_jδ_yδ_jρv_yv_j) = Σ_jδ_jρv_yv_j = ρv_yv、δ_z∙(Σ_jδ_zδ_jρv_zv_j) = Σ_jδ_jρv_zv_j = ρv_zv]

同樣地，通過法向量 n 的表面之總分子動量通量為 n∙π = pn + n∙τ。這是自表面負的那一側往正的那一側之通量，此量可以解釋成負的那一側材料通過表面施予正的那一側材料每單位面積之力。n∙π 的幾何解釋可見於 Problem 1D.2。

在本章，我們於 §1.2 定義動量的分子輸送，並已於本節描述動量的對流輸送。於第二章建立殼動量平衡 (shell momentum balances)，以及於第三章建立通用的動量平衡 (general momentum balance)，我們將會發現定義合併的動量通量 (combined momentum flux) 非常有用，它是分子動量通量和對流動量通量的和，即

(1.7-2)

記住 pδ 的貢獻並不含速度卻只有壓力，ρvv 這結合含有密度和速度分量的相乘，τ 含有黏度且對於牛頓流體是正比於速度梯度，以上所有量均為二階張量 (second-order tensors)。

大部分的時候我們將處理這些量的分量，例如，Φ 的分量為

(1.7-3a, 3b)

等等，平行於 Tables 1.2-1 和 1.7-1 的矩陣元素。需記住的重要事情為
𝜙_xy = 透過分子和對流機制，通過垂直 x 方向的表面之合併的 y 動量通量
這裡，第二個指標 (y) 是被輸送的動量分量，而第一個 (x) 是輸送的方向 (第一個指標亦可解釋成，垂直於第一個指標 (x) 方向的表面)。

用於動量通量的各種符號和專門用語整理於 Table 1.7-2，所有通量使用同樣的符號規定。

Reference: RB Bird, WE Stewart, EN Lightfoot, Transport Phenomena, 2nd ed (Wiley 2002).

§9.7 能量的對流輸送 (Convective Transport of Energy)

在 §9.1 我們已介紹傅立葉熱傳導定律 (Fourier's law of heat conduction)，它解釋了在介質中的能量輸送，其本質為分子運動 (molecular motions)。 

能量也可透過流體的整體運動 (bulk motion of the fluid) 輸送。在 Fig. 9.7-1 我們呈現在點 P 三個相互垂直且面積為 dS 的元素，其中流體的速度為 v，所以通過垂直 x 軸的表面元素 dS 之體積流率為 v_xdS，而正被掃過同樣表面元素之能量時變率則為

(9.7-1)

其中，ρv²/2 = ρ(v_x² + v_y² + v_z²)/2 是單位體積之動能，ρU^{^}是單位體積之內能。

內能在非平衡狀態 (nonequilibrium situation) 之定義需要小心處理，從連續體學 (continuum) 的觀點，在位置 r 及時間 t 的內能，被假設具有和平衡狀態下 (at equilibrium) 相同的局部瞬間密度和溫度函數 (function of the local, instantaneous density and temperature)；從分子的觀點，在小區域位置 r 及時間 t 的內能，為以下三項之總合，包括所有組成原子的動能 (kinetic energies of all the constituent atoms) (相對於流動速度 v)、分子內位能 (intramolecular potential energies)、分子間能量 (intermolecular energies)。

回顧 §0.3 討論之分子碰撞 (molecular collisions)，我們發現可將一對碰撞分子的能量 (the energy of a colliding pair of the molecules)，視為分子質量中心的動能總合 (the sum of the kinetic energies referred to the center of mass of the molecule) 加上分子間位能 (intramolecular potential energy)。這裡我們也將流體的能量 (視為連續體)，拆成整體流體運動的動能和內能，後者 (指內能) 包括分子相對於流體速度之分子動能，以及分子內和分子間位能。

對於正被掃過垂直 y 軸和 z 軸的兩個表面元素之能量時變率，我們可以寫下相似於 Eq. 9.7-1 的表示式，如果將三個個別表示式乘上對應的單位向量並相加，並經過除以 dS 後可得

(9.7-2)

這個量稱為對流能量通量向量 (convective energy flux vector)。為了得到通過垂直單位向量為 n 的單位表面之對流能量通量，我們得進行內積 n ∙ (ρv²/2 + ρU^{^})v，這是由表面之負側往表面之正側的通量，可以與 Fig. 1.7-2 的對流動量通量比較 (convective momentum flux)。

Reference: RB Bird, WE Stewart, EN Lightfoot, Transport Phenomena, 2nd ed (Wiley 2002).

2020 Macosko 流變學工作坊

§9.2 熱傳導率之溫度和壓力相依性 (Temperature and Pressure Dependence of Thermal Conductivity)

當特定物質的熱傳導率數據無法取得時，我們可以使用 Fig. 9.2-1 的對應狀態圖表 (corresponding-states chart) 進行估算。該圖是基於數個單原子 (monatomic) 物質的熱傳導率數據。與 Fig. 1.3-1 的黏度圖相似，Fig. 9.2-1 的圖是針對對比熱傳導率 k_r (= k/k_c)，k_r 為在壓力 p 和溫度 T 的熱傳導率 k 除上在臨界點 (critical point) 的熱傳導率 k_c。對比熱傳導率 k_r 的值被繪製成對比溫度 T_r = T/T_c 和對比壓力 p_r = p/p_c 的函數。Figure 9.2-1 雖是基於有限數量的單原子物質，卻可用於多原子 (polyatomic) 物質的估算，唯不可用於臨界點的附近。

由 Fig. 9.2-1 可發現，氣體的熱傳導率在低壓時接近一個 T 的極限函數；對大部分氣體，約在一大氣壓 (1 atm) 可達到這個極限。氣體在低密度時的熱傳導率隨著溫度升高而增加，然而，大部分液體的熱傳導率隨著溫度升高而下降。這個關聯性在液體區間 (liquid region) 則較不可靠；極性 (polar) 或締合 (associated) 液體 (例如，水)，可能在 k 對 T 的作圖具有一個最大值。不過，對應狀態圖的主要功能是讓我們大致了解氣體和液體之整體熱傳導率行為。

k_c 這個量可用以下任一方法估算：(i) 如果在已知對比溫度和壓力下，k 是已知的，我們可以從圖讀取 k_r，然後計算 k_c (=k/k_r)；(ii) 我們可以利用 §9.3 提供的方法，先估算在低密度區間 (low-density region) 的 k 值，然後再使用方法 (i)。透過方法 (i) 取得的 k_c 列於附錄 E。

對於混合物，熱傳導率之估算可以使用類比於 §1.3 提供的方法，然而，主要是因為在高壓 (elevated pressure) 的數據過少，所以對於假臨界步驟 (pseudocritical procedures) 用於熱傳導率之準確性了解甚少。

Reference: RB Bird, WE Stewart, EN Lightfoot, Transport Phenomena, 2nd ed (Wiley 2002).

§9.1 傅立葉熱傳導定律：分子能量輸送 (Fourier's Law of Heat Conduction: Molecular Energy Transport)

Revised: 2023/3/2

我們都知道有些材料非常容易導熱 (例如，金屬)，而有些則是熱的絕緣體 (例如，木頭)。描述熱傳導速率的物理性質是熱傳導率 k (thermal conductivity)。

熱在液體的傳導可以想成分子的能量輸送 (molecular energy transport)，儘管其基本的機制是組成分子的運動。能量也可以透過流體的整體運動 (bulk motion) 進行輸送，稱為對流能量輸送 (convective energy transport)，這種形式的輸送取決於流體的密度 ρ。另一種機制為擴散能量輸送 (diffusive energy transport)，它發生在相互間擴散 (interdiffusing) 的混合物。此外，能量也可透過輻射能量輸送 (radiative energy transport)，它的特色是不需要材料介質 (material medium)，但是前述的傳導、對流則需要。本章將介紹前兩種機制，即傳導和對流。輻射則在第 16 章介紹，擴散熱輸送則在 §19.3 和 §24.2 討論。

我們於 §9.1 利用傅立葉定律的熱通量向量 q (Fourier's law for the heat flux vector) 定義熱傳導率 k。在 §9.2 透過對應狀態的原理 (principle of corresponding states)，結論流體的 k 之溫度與壓力相依性。接著在後面的四個小節，我們介紹有關氣體、液體、固體、固體複合物 (composite solids) 的熱傳導率，並提供理論的結果。

因為在第 10、11 章我們將使用能量守恆定律 (law of conservation of energy) 建立問題，所以我們不僅需要知道熱如何進出系統，還需知道透過分子機制 (molecular mechanisms)，功 (work) 是如何施加於系統或系統如何作功。分子作功的項 (molecular work term) 之本質將於 §9.8 討論。最後，透過結合傳導的熱通量 (conductive heat flux)、對流的能量通量 (convective energy flux)、功通量 (work flux)，我們可以創造一個合併的能量通量向量 e (combined energy flux vector)，其對建立能量平衡 (energy balances) 相當有用。

§9.1 傅立葉熱傳導定律：分子能量輸送 (Fourier's Law of Heat Conduction: Molecular Energy Transport)

考慮一個面積為 A 的固態材料厚片，其介於距離為 Y 的兩個大平行平板之間。我們假想一開始時 (t < 0)，整個固體材料的溫度為 T₀。在 t = 0 時，下板突然升至較高的溫度 T₁，並維持在該溫度。隨著時間增加，厚片的溫度曲線逐漸改變，最終達到一個線性穩態的溫度分佈 (如 Fig. 9.1-1 所示)。當達到穩態後，需要一個固定的熱流率 Q 通過厚片，以維持溫度差 △T = T₁ - T₀。對於足夠小的 △T，下面的關係式成立

(9.1-1)

也就是，單位面積的熱流率正比於距離 Y 對應的溫度差。比例常數 k 是厚片的熱傳導率。如果兩板之間是液體或氣體，只要小心地消除對流和輻射，則 Eq. 9.1-1 也是成立的。



在接下來的章節中較適合使用上式的微分形式 (differential form)，也就是說，當厚片的厚度趨近於零，我們使用 Eq. 9.1-1 的極限形式 (limiting form)，而在正 y 方向的局部單位面積熱流率表示成 q_y，Eq. 9.1-1 因此變成

(9.1-2)

這個用來定義 k 的方程式是傅立葉熱傳導定律的一維形式，它說明傳導的熱通量正比於溫度梯度 (temperature gradient)，或者圖像式地來說，在溫度對距離的圖上，熱向下坡滑動。事實上，Eq. 9.1-2 並非一個自然定律，而是一個建議，不過，它已被證明是個非常有用的經驗式。在附錄 D 的討論可知，此方程式是具有理論基礎的。

如果溫度在三個方向均有變化，我們可以對每個座標方向寫下一個與 Eq. 9.1-2 相似的方程式

(9.1-3, 4, 5)

如果上面的每一個方程式都乘上適當的單位向量，並相加總的話，我們得到

(9.1-6)

這是三維形式的傅立葉定律。此方程式描述熱在均質 (或均向) 介質的分子輸送 (molecular transport of heat in isotropic media)。此處的均質 (或均向) 指的是材料不具有喜好的方向，所以在各方向的熱傳導具有相同的熱傳導率 k。

有些固體，例如單一非正方體晶體 (single noncubic crystals)、纖維材料 (fibrous materials) 和層板 (laminates) 都是非均質 (或非均向) 的 (anisotropic)。對於這類物質，我們必需以下式取代 Eq. 9.1-6

(9.1-7)

其中，κ 是對稱的二階張量 (symmetric second-order tensor)，稱為熱傳導率張量 (thermal conductivity tensor)。因此，熱通量向量和溫度梯度並沒有指向相同的方向。對於在剪切流場 v_x(y, t) 的高分子液體，其熱傳導率在 x 方向 (流動方向) 可能較平衡值高 20%，而在 z 方向減少 10%。填充床 (packed bed) 的非均向熱傳導將在 §9.6 討論。

另一個可以廣義化 Eq. 9.1-6 的方式，是類比於線性黏彈 Maxwell 模型 (Eq. 8.4-3)，增加一個含有 q 的時間導數 (time derivative of q) 乘上一個時間常數 (time constant) 的項，但是似乎很少實驗證據可以保證這個廣義化之正確性。

讀者將會注意到熱傳導 (heat conduction) 的 Eq. 9.1-2 和黏滯流動 (viscous flow) 的 Eq. 1.1-2 很相似，在這兩方程式中，通量均正比於負的巨觀變數之梯度 (negative of the gradient of a macroscopic variable)，以及比例係數是材料的特徵物理性質，並且與溫度和壓力有關。對於三維的輸送情況，我們發現熱傳導的 Eq. 9.1-6 和黏滯流動的 Eq. 1.2-7 看起來不太一樣，這差異之所以存在是因為能量是純量，但動量是向量，而且熱通量 q 是一個具有三個分量的向量，但動量通量 τ 是一個具有九個分量的二階張量。我們預期能量和動量的輸送除了在某些簡單幾何的情形外，數學上並不會類似。

除了定義於 Eq. 9.1-2 的熱傳導率 k，另一個常用的量為熱擴散係數 α (thermal diffusivity)，定義為

(9.1-8)

這裡的 C_p^{^} 是定壓下的熱容量 (heat capacity at constant pressure)，在符號上方的抑揚符號 (^) 表示每單位質量 (per unit mass)，有時我們會需要使用 C_p^~，波浪符號 (~) 表示每莫耳。

熱擴散係數 α 和動黏度 ν 具有相同的單位，即 (長度)²/時間。當假設物理性質為定值時，k 和 ν 這兩個量以同樣的方式出現於動量和能量輸送的改變方程式。ν/α 這個比值表示在流動系統中之動量與能量輸送之難易程度。此無因次比值

(9.1-9)

稱為 Prandtl 數 (Pr)。我們將在接下來幾章遇到另一個無因次群 Péclet 數 (Pé)；Pé = RePr。

熱傳導率和相關量的單位可見於 Table 9.1-1，其它的單位以及不同系統間的相互關係 (interrelations) 可以參考附錄 F。

熱傳導率可以自氣體的約略值 0.01 W/m∙K 一路變化至純金屬的約略值 1000 W/m∙K (差距十萬倍)。一些氣體、液體、液體金屬、固體的熱傳導率之實驗值可見於 Tables 9.1-2、9.1-3、9.1-4、9.1-5。在計算時應儘可能使用實驗值，如果缺少實驗數據的話，我們可以使用接下來幾節的方法估算或者查閱其它工程手冊。

Example 9.1-1 熱傳導率之量測

Reference: RB Bird, WE Stewart, EN Lightfoot, Transport Phenomena, 2nd ed (Wiley 2002).

牛頓法 (Newton's Method)

Reference: RL Burden, DJ Faires, AM Burden, Numerical Analysis, 10th ed (Cengage Learning 2016).