廣義牛頓流體 (Generalized Newtonian Fluids)

廣義的牛頓流體 (generalized Newtonian fluid; GNF) 是基於連續體力學 (continuum mechanics)，使用一個非常簡單的本質方程式 (constitutive equation) 補捉穩態下之剪切致稀 (shear thinning) 的非牛頓流體行為。

對於牛頓流體，黏度是個常數，不隨剪切速率張量而變，遵守牛頓黏度定律 (Newton's law of viscosity)

為了表現非牛頓流體剪切致稀的特徵，因此，在 GNF 中，黏度項被修正為剪切速率的函數如下


至於我們該如何決定 GNF 的本質方程式，也就是黏度的表示式呢? 原則有兩個，第一，表示式能與黏度曲線的實驗數據吻合；第二，表示式必需簡單易於計算。

以下我們將介紹黏度表示式的三種模型，分別為

(1) Power-law model (兩個參數)
(2) Carreau-Yasuda model (五個參數)
(3) Bingham model (兩個參數)

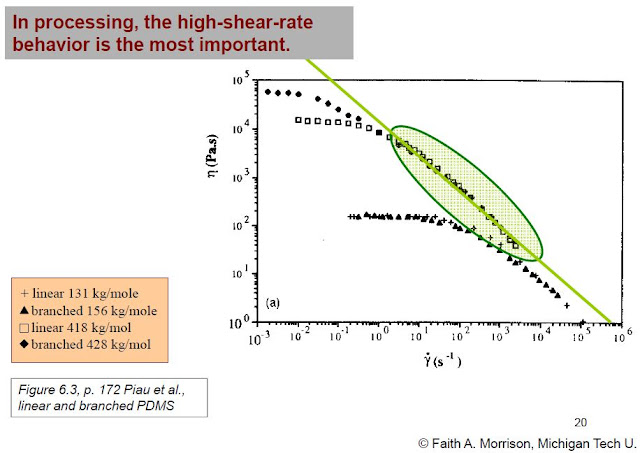
首先介紹 power-law model (冪次律模型)，非牛頓流體在高剪切率的加工製程中，剪切致稀的行為非常明顯，黏度可下降約 100 倍，如 Fig. 1。

Figure 1 剪切致稀行為

Power-law model 無法反應流體在低剪切率下的黏度 (也就是牛頓平台區)，但能補捉高剪切率區域黏度變化呈 power-law 型式之行為 (斜率為 n - 1)，，其數學表示式及曲線 (藍線) 如 Fig. 2，n 值一般介於 0.2 至 1 之間，m 值則取決於流體在高剪切率的黏度。

Figure 2 Power-law model

Figure 3 提供一個由壓力驅動的垂直管流為例子，這裡我們假設黏度的表示式為 Power-law model，並計算穩態下管內流速分佈，結果繪於 Fig. 4。

Figure 3

Figure 4

Figure 4 提供不同 n 值下的速度曲線，可以明顯觀察到不同剪切致稀程度 (即 n 值) 對曲線的影響。
當 n = 1，為牛頓流體 (黏度為定值)
當 n < 1，為非牛頓流體 (黏度呈 power law) 且曲線呈微幅塞流 (plug flow)
當 n ⟶ 0 ，為非牛頓流體且曲線呈明顯塞流 (plug flow)

Figure 5 為 GNF 的本質方程式，在剪切流場下，不管我們選擇何種黏度表示式，GNF 均不能預測剪切正向力，也就是無法解釋爬桿現象。

Figure 5

Figure 6 為 GNF 對於起動剪切流場的預測 (startup of shear flow)，我們可以發現圖左的實驗數據和圖右的 GNF 預測有個明顯差異，即實驗數據是緩慢地達到穩態值 (藍線)，這是流體彈性的重要表徵；反觀，GNF 的預測則是瞬間 (綠線)。之後我們會導入記憶效應於本質方程式中，補捉這個重要性質。

Figure 6

本文最後僅介紹 Carreau-Yasuda model 和 Bingham model 的黏度表示式，分別如 Figs. 7 和 8。前者可額外描述非牛頓流體在極低剪切速率下黏度為定值的行為；後者則適用於具有屈服應力 (yield stress) 的非牛頓流體。

Figure 7

Figure 8

Reference: Morrison, F. A., Understanding Rheology (Oxford University Press, New York, 2001).