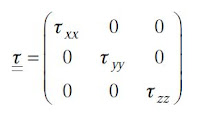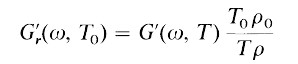共旋馬克斯威爾模型 (Corotational Maxwell Model) 於拉伸流 (Elongational Flow) 之預測

典型的拉伸流 (elongational 或 stretching flow) 常出現於紡絲 (fiber spinning) 製程，如 Fig 3.13 所示。其它型式的拉伸流也存在於薄膜吹製 (film blowing)、吹氣成形 (blow molding)、熱壓成形 (thermoforming) 等製程。這些類型的流場常被稱為無剪切流場 (shear-free flows)。

Figure 3.13 紡絲

若假設 z 軸為拉伸方向，單軸拉伸流場的速度梯度張量為 (velocity gradient of the velocity vector)

(1)

形變率張量 (rate of deformation tensor) 則為

(2)

在拉伸流場下，渦度張量 (vorticity tensor) 為零

(3)

故剪切力的共旋微分 (corotational derivative) 變成了實質微分 (substantial derivative)

(4)

即 Eq. 4 的第二項等於零，故剪切力的實質時間微分為

(5)

在上式中，應力張量為

(6)

於單軸拉伸流下 (uniaxial elongational flow)，流體的運動被定義為 (έ 為正值)

(6)

將 Eqs. 1 至 6，代入共旋馬克斯威爾模型

(7)

可得到穩態下之各正向力分量

(8)

為了描述兩種不同的正向力差值，可分別定義兩個獨立的黏度方程式 η₁ 和 η_2 如下

(9)

(10)

將 Eq. 8 的各個分量分別代入 Eq. 9 和 Eq. 10 後，可得

η₁ = 3η_{0     (11)}

η₂ = 0     ₍₁₂₎

由 Eq. 11 可得知，共旋馬克斯威爾模型正確預測拉伸黏度為 3 倍的剪切黏度。

Reference: T Osswald and N Rudolph, Polymer Rheology: Fundamentals and Applications (Hanser 2015). 

書籍 - 輸送現象之聖經 Transport Phenomena

化工系最重要的必修課程是 "單元操作與輸送現象"，此學科涵蓋了流體力學 (3 學分)、熱量傳遞 (3 學分)、質量傳遞 (4 學分) 三門課，共 10 學分。化工系的老師、學生都知道，"Transport Phenomena" 這本書可謂輸送現象的聖經。換句話說，作者群把此書寫得非常之好，但同時亦代表著較不易閱讀。主要是因為本書內容非常基礎，也從分子的角度出發，解釋巨觀的現象。另外，書中充滿大量的向量 (vector) 與張量 (tensor) 符號，非常的物理。不過對有心學好輸送現象的人來說，拜讀此書是必經之路。於 2002 年，作者 Bird、Stewart、Lightfoot 出了第二版的 Transport Phenomena；隨後於 2014 年，原作者群外加上 Klingenberg，發行了另一本書 Introductory Transport Phenomena。目前這兩本書同時發行，至於作者們為何想要在 2014 年出版 Introductory Transport Phenomena，便不得而知了。基本上，這本新書的內容和原來的 Transport Phenomena 相去不遠，僅針對一些推導細節加以闡述和更新一些章節內容。

輸送現象 (第二版，2002)

輸送現象簡介 (第一版，2014)

共旋馬克斯威爾模型 (Corotational Maxwell Model) 於簡單剪切流場 (Simple Shear Flow) 的預測

這裡我們檢驗一下共旋馬克斯威爾模型 (corotational Maxwell model) 於簡單剪切流場 (simple shear flow) 的預測。Corotational Maxwell 模型是線性黏彈性 Maxwell 模型之延伸，可視為非線性黏彈性的模型 (nonlinear viscoelastic model)。Maxwell 模型為

(1)

而 corotational Maxwell 模型為

(2)

Equations 1 與 2 唯一的差別是前者為時間偏微導數 (partial time derivative)，後者為共旋時間導數 (corotational time derivative)。相較於時間偏微導數，共旋時間導數的引入將滿足客觀性原則 (principle of objectivity)，即應力張量的表示將與流體單元在空間中的瞬間方向性無關 (the expression for the stress tensor should be independent of the instantaneous orientation of a fluid element in space)。在 Eq. 2 中，剪切應力張量 τ 的共旋時間導數為 τ₍₀₎ (= Dτ/Dt)，即 

(3)

其中，D/Dt 為時間實質導數 (substantial derivative)。於簡單剪切流場，速度梯度張量 (velocity gradient tensor) 為

(4)

渦度張量 (vorticity tensor) 為 ω = ▽∙u - (▽∙u)^T

(5)

 應力張量 (stress tensor) 為

(6)

速度向量的各分量為

(7)

應變率張量為 (rate-of-strain tensor or rate-of-deformation tensor) 

(8)

結合 Eqs. 2 至 7，以及應力張量不隨位置和時間而變的假設 (即 Eq. 3 的第一項時間實質導數 為零 Dτ/Dt = ¶τ/¶t + u_x¶τ/¶x + u_y¶τ/¶y + u_z¶τ/¶z = 0，但第二項 1/2{ω ∙ τ - τ ∙ ω} 不為零)，我們可得以下結果，黏度與剪切率的相依性為

(9)

Figure 5.27 為黏度對剪切率的作圖，相同於 Maxwell 模型，corotational Maxwell 模型預測了牛頓平台區 (Newtonian plateau)，但後者模型更成功預測實驗上常見的剪切致稀的行為 (shear thinning)。當 λ₀ 越大，剪切致稀將提前在低剪切率發生。另外，此模型對第一正向力差值 N₁ (first normal stress difference) 和其係數 ψ₁ (正值) 之預測為

(10)

 第一和第二正向力差值係數之理論比值為 (ψ₂ 負值)

(11)

實驗上，第二正向力差值較第一正向力差值難以測得，因此常以下式近似之

(12)

同時，Eqs. 10 和 11 告訴我們，corotational Maxwell 模型預測的第一和第二正向力差值異號且不為零。Figure 5.28 是第一正向力差值係數對剪切率的作圖，隨著剪切率越大，正向力差值係數越小。

雖然 corotational Maxwell 模型錯誤預測程度過大的剪切致稀行為 (excessive shear thinning；即在剪切率為 1/λ₀ 1/s 時，Equation 9 預測應力將有最大值) 和過大的正向力差比值 (實驗值約 - 0.1 至 - 0.4，而非 - 0.5)，但是僅有兩個參數的 corotational Maxwell 模型 (λ₀ 和 η₀)， 已可定性補捉低剪切率之流動行為，並幫助我們學習處理更進階的非線性黏彈模型。

Figure 5.27 Corotational Maxwell 模型對黏度之預測

同 Figure 5.27

Figure 5.28 Corotational Maxwell 模型對第一正向力差值係數之預測

同 Figure 5.28

Reference: T Osswald and N Rudolph, Polymer Rheology: Fundamentals and Applications (Hanser 2015). 

溫度對物質函數的影響 (Effects of Temperature on Material Functions)

Revised: 2022/4/12

流體的物質函數 (material function) 隨所處物理狀態而變，例如濃度、溫度和壓力。如 Fig. 3.3-1 所示，LDPE 熔體 (low-density polyethylene melt) 的黏度受溫度影響甚鉅，當溫度由 388 升至 513 K，零剪切率黏度 (zero-shear-rate viscosity) 下降約兩個數量級 (100 倍)。

值得注意的是，不同溫度下的黏度曲線具有非常相似的外形，而這個高度相似性，提供了一個重要經驗方法 (empirical method) 之根基，被稱之為對比變數方法 (method of reduced variables)，透過這個方法，可結合不同溫度下的黏度曲線，取得一條參考溫度之寬廣的主曲線 (master curve)，故此方法又可稱作時間溫度疊加原理 (time-temperature superposition principle, TTSP)。附帶一提，TTS 僅適用於熱流變學簡單的材料 (thermorheologically simple)，也就是適用於不會因溫度變化而產生微觀結構變化之材料。例如，TTS 適用玻璃轉化溫度以上的非結晶 (amorphous) 高分子 (例如，PMMA 或 PS)，但是對於半結晶 (semi-crystalline) 高分子 (例如，PEEK)，適用的溫度範圍會窄很多。

不同溫度下，LDPE 黏度對剪切率之作圖

為了從 log η vs. log γ̇  圖上不同溫度的黏度曲線，得到任一參考溫度 T₀ (reference temperature) 下之黏度主曲線 ，我們遵守以下兩個步驟：

一、 將溫度 T 的曲線垂直向上平移一個量 (若為負值，則為向下)

[註：請注意這裡是對零剪切黏度 η₀ 進行垂直平移操作]

二、將步驟一的黏度曲線再進行水平向右平移，使之重疊於參考溫度 T₀ 的曲線，η(γ̇ , T) 的水平平移量為 log a_T (若為負值，則為向左)，一般而言，移動因子為

(1)

對比變數方法預測，如果我們依照上述兩步驟分別將數據進行以下的處理：

(2)

和

(3)

最後將對比黏度 η_r (reduced viscosity) vs. 對比剪切率 (reduced shear rate) 作圖，便可獲得一條黏度主曲線。Figure 3.3-2 的黏度主曲線便是透過平移 Fig. 3.3-1 不同溫度下的曲線而來。一般而言，主曲線可以讓參考溫度下的實驗數據範圍加以擴大，只是在 Fig. 3.3-2 的例子不是那麼明顯而已。

LDPE 黏度與第一正向力係數之主曲線

兩種指數型方程式常被用來描述高分子熔體平移因子 a_T 之溫度相依性，如 Figures 3.6-1 和 3.6-2 所示，前者為阿瑞尼斯 (Arrhenius)，後者為 WLF。阿瑞尼斯方程式的表示式為

(4)

阿瑞尼斯適用於描述低分子量的流體或高於玻璃轉移溫度 (T_g) 100 K 以上之高分子熔體。WLF 方程式的表示式則為

(5)

WLF 適用於實驗溫度介於 T_g 和 T_g + 100 之間的高分子。如果參考溫度 T₀ 被定為 T_g，Equation 5 中的兩個可調參數的值約為

(6)

[註：常見的做法是令 T₀ = T_g、c₂⁰ = 51.6 K，故 WLF 變成單一參數之擬合]

另一種參數決定的作法為，先任意選定一個實驗上的參考溫度 T₀，兩個可調參數的值可先定為

(7)

畫上實驗的數據點於 Fig. 3.6-2 後，再微調 Eq. 7 中的兩個參數，以得到最好的擬合，也就是使 Fig. 3.6-2 的數據點儘量呈線性，以符合 WLF 方程式的預測。

Arrhenius 作圖

WLF 作圖

事實上，我們更常對線性黏彈的數據 (而不是黏度) 進行主曲線的建立，以下將進行介紹。由 Eqs. 2 和 3 亦可定義對比剪切應力 (reduced shear stress) 如下 (即 τ_r 等於 Eq. 2 乘以 Eq. 3)

(8)

由 Eq. 8 可知，τ_yx 對溫度相當不敏感 (這裡指垂直平移的量不偌水平平移的量來得那麼大)，而且可以在未知 a_T 的情況下進行垂直平移。對不同的 τ_r(γ̇ , T₀) 曲線進行水平平移，將可得到主曲線 τ_r(γ̇ _r, T₀)。一但取得主曲線後，我們可以繪製 η_r (= - τ_r/γ̇ _r) vs. γ̇ _r 的圖。

類比於對比剪切應力 τ_r，對比儲存模數 (reduced storage modulus) 和對比損耗模數 (reduced loss modulus) 可分別定義成

(9)

和

(10)

Figure 3.4-3 即是透過平移後得到 LDPE 的儲存與損耗模數主曲線，因為流變儀能提供的頻率範圍僅為 10^-2 到 10² Hz (三個數量級)，但主曲線能將範圍延伸至 10^-3 到 10⁴ Hz (七個數量級)。

LDPE 儲存與損耗模數之主曲線，參考溫度為 423 K

然而，實際在處理實驗數據時，我們並不知道各個量測溫度 T 對應的密度 ρ，所以一般的作法是透過手動平移，得到參考溫度 (T₀) 的平滑主曲線，以下為執行的步驟:
一、選定一個參考溫度 T₀，以此溫度對應之數據 (G' 和 G") 為基準。
二、針對溫度 T 對應之數據 (G' 和 G")，分別進行水平和垂直的平移，得到平滑且部分重疊於 T₀ 數據的曲線，記錄下水平平移因子 a_T 和垂直平移因子 b_T。
三、針對其它溫度的數據，重覆執行步驟二，得到對應之水平與垂直平移因子。
四、將上述實驗取得之水平平移因子 a_T，據 Fig. 3.6-2 的座標作圖，並確認實驗數據點呈一直線 (表示滿足 WLF 關係式)；垂直平移因子 b_T 大都在 1 的上下變動，一般並未對之進行處理。
五、可由 Fig. 3.6-2 之作圖中，取得截距與斜率，由 WLF 方程式可知 (Eq. 5)，截距為 c₂⁰/c₁⁰，斜率為 1/c₁⁰。
六、步驟五已取得參考溫度 T₀ 對應之 c₁⁰、c₂⁰，所以現在透過 Eq. 5 可以得到任一溫度 T 對應之 a_T。接著將參考溫度的主曲線水平平移 a_T 後，即得該溫度 T 之主曲線。為了得到更精確之主曲線，需結合步驟三記錄之垂直平移因子 b_T，進行垂直方向的微調。

現今流變儀搭配的軟體大多能以自動化的方式得到參考溫度的主曲線，例如 TA Instruments 的 TRIOS 軟體便可於一分鐘內快速取得平滑的主曲線，同時也可取得 WLF 的參數，除了節省我們相當多的時間外，最終 TTS 的結果亦不會因人而異。
 

Figure 8.15 便是透過手動方式平移得到的 PVME 熔體振盪剪切數據。此主曲線涵蓋非常寬廣的頻率範圍 (10^-10 到 10² Hz)，共 12 個數量級 ，因此我們才有機會清楚看到高分子多尺度的鏈鬆馳運動 (非常局部到整體)，也就是自 Kuhn 單體 (Kuhn monomer) 到纏結鏈 (entanglement strand) 再到整條高分子鏈，這些尺度所對應的分子運動時間尺度為 0.3 ns 到 0.1 μs 再到 0.2 s。

PVME 儲存與損耗模數之主曲線，參考溫度為 -24°C。右側插圖為各個溫度下的原始數據

Reference: RB Bird, RC Armstrong, O Hassager, Dynamics of Polymeric Liquids, Vol. 1, Fluid Mechanics, 2nd ed (Wiley-Interscience 1987).

示差掃描熱量分析儀 (Differential Scanning Calorimetry, DSC) 決定比熱容、相變溫度、結晶溫度

示差掃描熱量分析儀 (differential scanning calorimetry; DSC) 可以讓我們得到以下幾個物理量，(1) 比熱容 (C_p, specific heat capacity) 對溫度的相依性；(2) 一階相變發生的溫度；(3) 焓 (H, enthalpy) 於相轉變過程的改變量 (dH = dQ = C_pdT) 或結晶度 (degree of crystallinity)；(4) 聚合反應 (polymerization) 涉及放熱的交聯化過程。常見的溫度掃描速率為 10-20C/min。

單位質量的物質於固定壓力下的比熱容 C_p (specific heat capacity) 定義如下

(1)

其中 dQ/dt 是能量 Q 供給樣品的速率，dT/dt 是溫度 T 上升的速率。如果溫度上升速率 dT/dt 維持定值 k，則 dQ/dt (= kC_p) vs. T 的作圖可得知任何溫度的熱容。如 Fig. 2.1a 所示，y 軸等於 dQ/dt，而尖峰代表發生一階相變 (first-order phase transition)，例如熔化 (melting)，於此溫度下之 dQ/dt 變成無窮大而難以進行數據分析。

Figure 2.1 dQ/dt vs. t。(a) 樣品直接被加熱 (量測樣品的溫度)；(b) 樣品透過試樣盤間接被加熱 (量測試樣盤的溫度)。

為了克服上述數據分析的困難，實驗的作法並不是直接量測樣品的溫度，而是將樣品置於試樣盤 (sample pan)，量測試樣盤的溫度。這樣的作法帶來兩個好處，(1) 試樣盤將有其自身的比熱，可獨立於樣品的比熱；(2) 熱量自試樣盤傳遞至樣品，故兩者的溫度將會有一個滯延 (lag)。因此，當發生一階相變時，dQ/dt vs. T 的作圖將變成 Fig. 2.1b 所示，曲線下的面積 A 正比於相變化過程中所需總能量，而焓的改變量 △H 為 (一般定義為每單位質量所需能量)

△H = A/kw = C_p△T     (2)

其中，k 為升溫速率、w 為樣品重量 (約為 5-15 mg)。由 Eq. 2 可知，△H 已經被升溫速率歸一化 (normalized)，對簡單材料而言，當升溫速率差異不大時，△H 的值應該相當接近。

Figure 2.2 是商業化 DSC 儀器的圖示，工作原理為比較供予樣品 (S) 與無樣品 (R) 的能量差異，故同時配置獨立的樣品加熱器 (sample heater) 與基準加熱器 (reference heater)。Figure 2.3 是熱塑性聚酯 (polyester) 的 DSC 數據，可據此決定聚酯之玻璃轉化溫度 (glass transition temperature, T_g)、結晶溫度 (crystallization temperature, T_c)、熔點 (melting point, T_m) 等性質。其中，結晶為一放熱過程 (exothermic process)。

Figure 2.2 DSC 儀器。左為樣品盤 (S)，右為參考基準盤 (R)。

Figure 2.3 聚酯的 DSC 數據

Reference: D. I. Bower, An Introduction to Polymer Physics (Cambridge University Press, 2002).