我們考慮的第一個系統是圓截面具半徑 R 和導電率 (electrical conductivity) ke ohm-1cm-1 的電線 (electrical wire),通過這條線的電流密度 (current density) 為 I amp/cm2。電流的傳輸是一個不可逆過程,所以一些電能將被轉換成熱 (熱能),每單位體積之熱生成率可表示成
對於能量平衡,我們將厚度 △r 和長度 L 的圓柱殼視為一個系統;見 Fig. 10.2-1。因為沒有流動的流體,故此系統的速度為零 (即 v = 0),唯一對能量平衡的貢獻為
qr 這個符號表示 "在 r 方向的熱通量",而 (∙∙∙)|r=r+Δr 表示 "在位置 r+Δr 估算"。特別注意我們進、出定義為正的 r 方向。

我們把這些量代入 Eq. 10.1-1 的能量平衡,除以 2πLΔr 並 Δr 讓趨近於零

我們把這些量代入 Eq. 10.1-1 的能量平衡,除以 2πLΔr 並 Δr 讓趨近於零
表示式左側是 rqr 對 r 的一階導數,因此 Eq. 10.2-5 變成
這是能量通量的第一階微分方程式,可積分得到下式
因為以下這個邊界條件,積分常數 C1 必需是零
B.C. 1: r = 0 , r 方向的熱通量 qr 不是無窮大 (10.2-8)
因此,熱通量分佈最後的表示式為
這說明熱通量隨 r 線性增加。
我們接著接傳立葉定律 qr = -k(dT/dr) 代入 Eq. 10.2-9,並得到
當 k 被假設為定值,這個一階微分方程式可被積分得到
因此,C2 = (SeR2/4k) + T0。Equation 10.2-11 變成
Equation 10.2-13 是自電線軸中心至位置 r 之溫度上升抛物線函數 (在 r = 0,溫度最高;r = R,溫度最低,為 T0)。
(i) 溫度上升量之最大值 (maximum temperature rise),發生於金屬電線的中心軸 (在 r = 0)
(ii) 溫度上升量之平均值為 (average temperature rise)
因此,平均截面的溫度上升量為最大溫度上升量之一半。
(iii) 電線表面 (r = R) 的熱流出率 (heat outflow) (對於線長 L)
這個結果並不意外,因為在穩態時,體積 πR2L 內因電耗散 (electrical dissipation) 生成的熱必需經由表面 (r = R) 離開。
當讀者歷經上述推導過程,可能會有一種已經看過的感覺 (the feeling of déjà vu)。被加熱線的問題和圓管黏滯流動的問題之間有明顯的相似性 (similarity),唯符號有點不同
也就是當這些量被適當選擇,兩個問題的微分方程式和邊界條件是相同的,且這些物理過程 (physical processes) 被稱之為類同的 (analogous)。並非所有動量傳遞的問題都有類比 (analogs) 於能量和質量輸送。然而,當這樣的類比被找到後,它們可能會非常有用,因為可以自一個領域接管已知結果,然後應用在另一個。例如,對於一個在傾斜平面之液體薄膜黏滯流動(viscous flow in a liquid film on an inclined plane),讀者應該可以找到其熱傳導的類比。
在電工業,有很多熱傳導問題的例子。電機械 (electrical machinery) 內溫度上升之最小化將延長絕緣壽命 (insulation life),例如,使用內部液體冷卻定子導體 (liquid-cooled stator conductors) 在非常大的交流發電機 (AC generators)。









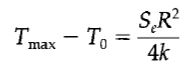



沒有留言:
張貼留言