典型的拉伸流 (elongational 或 stretching flow) 常出現於紡絲 (fiber spinning) 製程,如 Fig 3.13 所示。其它型式的拉伸流也存在於薄膜吹製 (film blowing)、吹氣成形 (blow molding)、熱壓成形 (thermoforming) 等製程。這些類型的流場常被稱為無剪切流場 (shear-free flows)。
 |
| Figure 3.13 紡絲 |
若假設 z 軸為拉伸方向,單軸拉伸流場的速度梯度張量為 (velocity gradient of the velocity vector)
形變率張量 (rate of deformation tensor) 則為
在拉伸流場下,渦度張量 (vorticity tensor) 為零
故剪切力的共旋微分 (corotational derivative) 變成了實質微分 (substantial derivative)
即 Eq. 4 的第二項等於零,故剪切力的實質時間微分為
在上式中,應力張量為
於單軸拉伸流下 (uniaxial elongational flow),流體的運動被定義為 (έ 為正值)
將 Eqs. 1 至 6,代入共旋馬克斯威爾模型
 (7)
(7)
可得到穩態下之各正向力分量
為了描述兩種不同的正向力差值,可分別定義兩個獨立的黏度方程式 η1 和 η2 如下
將 Eq. 8 的各個分量分別代入 Eq. 9 和 Eq. 10 後,可得
η1 = 3η0 (11)
η2 = 0 (12)
由 Eq. 11 可得知,共旋馬克斯威爾模型正確預測拉伸黏度為 3 倍的剪切黏度。
Reference: T Osswald and N Rudolph, Polymer Rheology: Fundamentals and Applications (Hanser 2015).




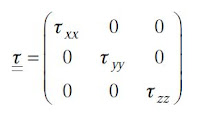




沒有留言:
張貼留言