似線性黏彈性模型 (Quasi-Linear Viscoelastic Model): Part 2

Convected Jeffreys 模型有三個參數，分別為零剪切率黏度 η₀、鬆馳時間 λ₁、延遲時間 λ₂。模型的本質方程式為

(1)

本文將針對 convected Jeffreys 模型，分別推導 (a) 於零剪切流 (shear-free flow) 下之時間相依本質方程式；(b) 穩態平面拉伸流 (planar and elongational flow) 之起始物質函數；(c) 穩態物質函數。

a. 零剪切流 (shear-free flow) 下之時間相依本質方程式

根據文末文獻的附錄 C，τ₍₁₎、γ₍₁₎、γ₍₂₎ 於非穩態零剪切流的張量表示式列於 Table C.1

Table C.1

將 Table C.1 代入 convected Jeffreys 模型 (Eq. 1)，可得到應力張量分量的非耦合常微分方程式 (uncoupled, ordinary differential equations for the stress tensor components)

(2, 3)

τ_yy 的方程式和 τ_xx 相同，只差在 Eq. 2 的 + b 需被 - b 取代。

b. 穩態零剪切流之前的起始過程

於穩態零剪切流之前的起始過程，拉伸率 (elongation rate) 可以使用 Heaviside 單位階梯函數 H(t) (Heaviside unit step function) 表示，即

(4)

其中，έ₀ 是常數。若將 Eq. 4 代入 Eq. 2，可得

(5)

其中，Dirac delta 函數 δ(t) 的引入是因為其為階梯函數的導數 (dH/dt = δ(t))，將 Eq. 5 自 t = 0^- (τ_xx = 0) 積分至任一時間 t > 0，可得

(6)

類似地，τ_yy 則是將 Eq. 6 的 + b 置換成 - b。而 τ_zz 則是

(7)

一個很有趣的結果是，如果當 λ₁έ₀ 的乘積值是下方的情況時，Equations 6 和 7將不會達到穩態。

(8)

無剪切流主要分三種，(i) 拉伸流 (elongational flow; b = 0, έ₀ > 0)；(ii) 雙軸拉伸流 (biaxial stretching flow; b = 0, έ₀ < 0)；(iii) 平面拉伸流 (planar elongational flow; b = 1)，b 的範圍在 0 到 1 之間。排除 Eq. 8 的情況，當 - 1/(1 + b) < λ₁έ₀ < 1/2，應力成長物質函數將有穩態值如下

(9)

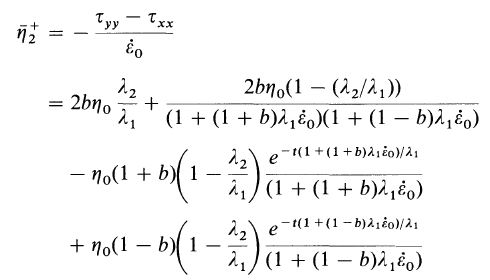(10)

c. 穩態零剪切流之物質函數

對於穩態零剪切流，應力值將很容易計算，因為統御微分方程式 (Eqs. 2 和 3) 將成為代數 (algebraic) 方程式。對於任何值的 έ₀，可得

(11, 12)

需注意的是，處於 Eq. 8 的情況時，穩態物質函數將成無窮大。

Reference: RB Bird, RC Armstrong, O Hassager, Dynamics of Polymeric Liquids, Vol. 1, Fluid Mechanics, 2nd ed (Wiley-Interscience 1987).