Welcome Message
「流行起於高分子,變化盡藏微宇宙」! 歡迎光臨「流變學好簡單 | The RheoMaster」部落格,成立於 2019/2/22,旨在提供簡單的中文流變學知識,包括高分子流變學、輸送現象、高分子加工、流變量測等。您可至右方進行關鍵字搜尋,若有任何建議,請至文章留言或來信 yuhowen@gmail.com。
Welcome to "The RheoMaster" Blog. This website was established in Feb 2019. In view of the lack of Chinese literature on rheology, here we offer basic knowledge relevant to polymer rheology, transport phenomena, polymer processing, rheometry, etc. If you have any suggestion, please leave a message on the post you are reading or email us at yuhowen@gmail.com.
2019年8月31日
2019年8月27日
微分黏彈模型 (Differential Viscoelastic Models)
於高分子加工中,流體材料通常經歷很大的形變 (large deformations),因此需要使用非線性黏彈模型 (nonlinear viscoelastic models) 描述流體的行為。黏彈模型有兩種型式,分別為微分型 (differential type) 和積分型 (integral type),以下簡短介紹微分型。
傳統上,微分型式的模型常被用來描述高分子於複雜流動系統的黏彈行為,很多微分型黏彈模型可以用下方一般式表之
其中,τ(1) 是軸差應力張量 (deviatoric stress tensor) 的第一反變對流時間導數 (first contravariant convected time derivative),它代表相對於與流體一同移動和變形的對流座標系統之變化率 (rates of change w.r.t. a convected coordinate system that moves and deforms with the fluid),τ(1) 定義如下
對於常被用來模擬高分子流動的各種黏彈模型,Table 1 整理了 Eq. 1 中的常數。以下針對各種黏彈模型進行簡要描述。
Upper convected Maxwell 模型和 White-Metzner 模型非常相似,只是後者額外考慮剪切率對鬆弛時間 (relaxation time) 和黏度 (viscosity) 的效應。兩種模型預測第二正向力係數為零。
Giesekus 模型 [1982] 是以分子為基礎而且應力是非線性的,計算時僅需三個參數 (零剪切率黏度、鬆弛時間、α),便可以描述冪次律區間 (power-law region),黏度和第一、第二正向力係數隨剪切率增加而導致的剪切致稀行為 (shear thinning behavior),Giesekus 模型亦能給予拉伸黏度、複數黏度合理的描述。Bird 等學者賦予這個模型分子角度之解釋,即 Giesekus 模型是一個以虎克啞鈴 (Hookean dumbbells) 為分子模型描述組成高分子行為之平均場理論 (mean-field theory)。
Phan-Thien and Tanner (PTT) 模型 [1977] 有四個參數,是自網狀結構理論 (network theory) 引伸而來的,而且應力也是非線性的。Giesekus 模型預測拉伸黏度隨拉伸率 (elongation rate) 單調遞增,而 PTT 模型則預測拉伸黏度存在一個最大值。目前為止,Giesekus 模型和 PTT 模型已被成功且廣泛應用於模流計算。
 |
| Table 1 Equation 1 的常數定義 |
Reference: T Osswald, JP Hernandez-Ortiz, Polymer Processing: Modeling and Simulation (Hanser 2006).
靜態高分子熔體之結晶動力學 (Crystallization Kinetics in Quiescent Melts)
高分子的結晶過程會生成球晶 (spherulite;見 Fig. 10.6),而球晶自晶核 (nuclei) 開始的成長過程,可被視為半徑逐漸增大的球 (sphere),若 G(t) 表示於時間 t 的球半徑成長速率,則在時間 s 和 t 之間生成的球之體積為
假設在時間 t,單位體積的晶核數為 Nq(t),且球晶體積之成長過程不受阻礙,則球晶體積分率 φ(t) 為
其中,Nq_dot(t) 為單位體積內晶核數目的生成速率。若假設球晶的半徑成長速率 G(t) 與晶核數目的生成速率 Nq_dot(t) 均為定值 (即 G(t)= G、Nq_dot(t) = Nq_dot),φ(t) 為
Equation 3 所計算的 φ(t) 稱為虛擬體積分率 (fictive volume fraction)。Avrami 提出,若晶核在成長過程中是均勻分散在整個體積時,真實 (actual) 的體積分率 α 可以透過以下簡式求得
晶核成長 (nucleation) 可分偶發晶核成長 (sporadic nucleation) 和瞬間晶核成長 (instantaneous nucleation),前者指晶核之出現是在隨機的位置 (random points) 且以有限的成長速率隨機發生的 (random times),故也稱為均勻晶核成長 (homogeneous nucleation)。後者指晶核之出現僅在一開始的瞬間,之後便維持一個固定的晶核數目密度 N0 (nuclei number density),故也稱為非均勻晶核成長 (heterogeneous nucleation)。
結晶動力學常使用 Avrami 方程式描述,即
α = 1 - exp(-ktn) (5)
其中,k 為 Avrami 等溫結晶速率常數 (isothermal crystallization rate constant),n 為 Avrami 指數 (index)。
對於偶發晶核成長,結合 Eqs. 3 和 4,我們可以得到 φ(t) 隨時間的變化為 (G(t)、Nq_dot(t) 為定值)
對於瞬間晶核成長,若起始的晶核數目密度為 N0,φ(t) 則為
由 Eqs. 6 和 7 可知,偶發晶核成長之 n = 4;瞬間晶核成長之 n = 3。實驗上觀測到的 n 值常介於 3 到 4 之間。Figure 3.20 是 PET 在不同溫度下的等溫結晶 (isothermal crystallization) DSC 數據,在結晶過程中,其斜率 (n) 大致可視為定值,但並非整個過程均是如此。
 |
| Figure 3.20 PET 之等溫結晶 DSC 數據,mc 為結晶質量 (crystallized mass),m0 為總質量 (total mass) |
值得注意的是,這裡指的真實球晶體積分率 α 應解釋為已結晶的體積 (crystallized volume) 占全部可結晶的體積 (total crystallizable volume) 之比例,故稱為相對結晶度 (relative crystallinity),α 的值介於 0 到 1 之間。
接下來介紹球晶成長速率 (growth rate of spherulites),對於一個球晶,其徑向成長率 G(T) 隨溫度的關係,可使用 Hoffman-Lauritzen 理論計算 [1960]
其中,U* 是運動活化能 (= 6,270 J/mol for PP),Rg 是氣體常數,T∞ = Tg - 30 是結晶完全停止的溫度,Tm0 是平衡熔化溫度 (equilibrium melting temperature),
Tm0 = Tr + b6p (9)
其中,Tr 是在參考壓力之平衡熔化溫度,b6 是 Tait 方程式描述 pvT 數據的參數,p 是壓力。△T = Tm0 - T 是過冷度 (supercooling)。至於不同溫度下之半徑成長速率 G(T) 該如何取得?一般是透過顯微鏡 (microscope) 進行球晶大小隨時間之影像分析 (如 Fig. 10.6)。有了 G(T) 的數據後,可透過繪製 [lnG + U*/(Rg(T - T∞))] 對 [(T + Tm0)/(2T2△T)],求得 G0 和 Kg 之參數。
 |
| Figure 10.6 iPP 等溫結晶之球晶大小影像分析 |
晶核數目的生成可由下式表之
N = N0 + Nf (10)
其中,N0 是在靜態 (quiescent) 時活化的晶核數目,而 Nf 是在流動時誘發 (flow-induced) 的晶核數目。一般而言,在靜態時,N0 隨過冷度 △T (= Tm0 - T) 增加而變大;在流動時,我們引入一個微分方程式描述 Nf 如何受剪切率和流體鬆弛時間等因子而改變。
Reference: PK Kennedy, R Zheng, Flow Analysis of Injection Molds, 2nd ed (Hanser 2013).
2019年8月21日
淺談流變儀之裝置 (Introduction to Set-up of Rheometers)
早在西元 1800 年左右,也就是 200 多年前,便有人開始發展流變儀。黏度計 (viscometer) 和流變儀 (rheometer) 是兩種常見的儀器,不過兩者之間的差異並沒有嚴格的定義。但是,一般而言,對於僅能進行速度或剪切速率控制之儀器 (speed- or shear rate-controlled),由於功能僅為黏度量測,因此我們習慣稱之為旋轉黏度計 (rotational viscometer),簡單的黏度計常被公司用來進行進出貨品之品質管控 (quality control)。 對比於黏度計,設計複雜的旋轉流變儀 (rotational rheometer) 除了可以額外進行力矩或剪切應力控制 (torque- or shear stress-controlled) 之旋轉實驗,也可以進行潛變 (creep)、鬆弛 (relaxation)、振盪 (oscillatory) 等實驗。以價格來說,流變儀約是黏度計的 6-10 倍或高。此外,流變儀可安裝各式各樣的模組配件,進行高溫、光學、拉伸流、扭力等實驗,因此流變儀可謂當前最新技術的整合 (state of the art)。市售流變儀主要來自兩家儀器製造商,分別為美國的 TA Instruments 和奧地利的 Anton Paar。
如 Fig. 11.6 所示,流變儀主要的機構有馬達 (motor, Mo)、軸承 (bearing, Be)、位置感測器 (position sensor, PS)、量測系統即夾具 (measuring system, MS)、控制器 (controller, Co),重要的量測性質包括最原始的偏轉角度 φ (deflection angle)、旋轉速度 n (rotational speed)、力矩 M (torque)。流變儀的機構設計可分為三種,第一種剪切速率 (或應變) 控制型 (shear rate- or strain-controlled) ,即預設輸入為 φ 或 n,偵測 M (Fig. 11.6 圖左)。第二種為剪切應力 (或力矩) 控制型 (shear stress- or torque-controlled),即預設輸入為 M,偵測 φ 或 n (Fig. 11.6 圖中間)。對於前面二種設計,均屬單頭系統 (single head system),驅動單元 (馬達) 和偵測單元 (傳感器 (transducer)) 被整合成一個單元。第三種為雙頭系統 (dual heads system),下方為驅動單元 (drive),透過馬達控制應變或剪切速率,即預設輸入為 φ 或 n,而上方偵測單元 (detector) 透過傳感器 (transducer) 測得 M (Fig. 11.6 圖右)。於雙頭系統,下方為轉子 (rotor),上方為定子 (stator),定子是靜止的或者可被偏轉極其有限的角度 (deflected to a very limited degree),偏轉的程度將取決於力矩傳感器 (torque transducer) 之剛性 (stiffness; 約 1 N/μm)。
Figures 11.7 和 11.8 分別為剪切應力控制 (shear stress-controlled) 和剪切速率控制 (shear rate-controlled) 模式流變儀的控制迴路 (control loops)。於 Fig. 11.7 的剪切應力控制迴路中,預設輸入 (input) 為 M or τ,電子控制器提供馬達一個適當的操作電流 I,使馬達產生對應的 M 於量測系統的樣品,造成偏轉角度 φ,並為位置感測器所記錄 (脈衝計數),最終輸出 (output) 為應變 γ 或剪切速率 γ_dot。因為摩擦總是存在,例如,軸承的摩擦阻力、運動中質量的慣性力 (包括旋轉夾具和樣品),這些擾動必需在實驗進行前透過電子控制器修正之。於 Fig. 11.8 的剪切速率控制迴路中,預設輸入 (input) 為 φ or γ,電子控制器也是同樣提供馬達一個適當的操作電流,使馬達產生對應的力矩 M 於量測系統的樣品,由位置感測器記錄實際的 (actual) 偏轉角度 φact。大部分的情況下,實際的 φact 將不同於輸入的 φ,所以經過電子控制器比對兩者的差異後,決定是否採用當下的力矩,如果差值過大,將進入一個封閉的控制迴路 (closed control loop),直到實際偏轉角度等於輸入偏轉角度,最終輸出 (output) 所需力矩或剪切應力。
最後討論一下軸承 (bearing),軸承用於連接旋轉軸 (rotation axis) 和靜止的機座 (stationary housing),有滾珠軸承 (ball bearing) 和空氣軸承 (air bearing) 兩種。我們必需特別注意的是,流變儀測得的總力矩 Mtot (total torque) 是以下各成份的相加
Reference: TG Mezger, The Rheology Handbook, 3rd ed (Vincentz 2011).
 |
| DHR 流變儀及各種配件 (TA Instruments) |
 |
| MCR 流變儀及各種配件 (Anton Paar) |
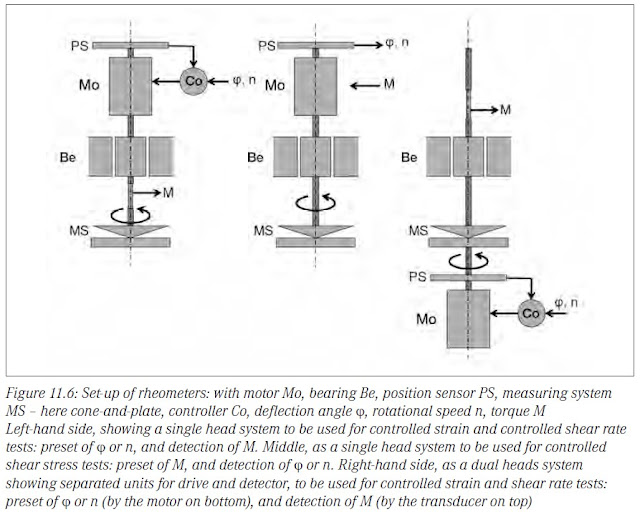 |
| Figure 11.6 三種不同設計的流變儀 |
如 Fig. 11.6 所示,流變儀主要的機構有馬達 (motor, Mo)、軸承 (bearing, Be)、位置感測器 (position sensor, PS)、量測系統即夾具 (measuring system, MS)、控制器 (controller, Co),重要的量測性質包括最原始的偏轉角度 φ (deflection angle)、旋轉速度 n (rotational speed)、力矩 M (torque)。流變儀的機構設計可分為三種,第一種剪切速率 (或應變) 控制型 (shear rate- or strain-controlled) ,即預設輸入為 φ 或 n,偵測 M (Fig. 11.6 圖左)。第二種為剪切應力 (或力矩) 控制型 (shear stress- or torque-controlled),即預設輸入為 M,偵測 φ 或 n (Fig. 11.6 圖中間)。對於前面二種設計,均屬單頭系統 (single head system),驅動單元 (馬達) 和偵測單元 (傳感器 (transducer)) 被整合成一個單元。第三種為雙頭系統 (dual heads system),下方為驅動單元 (drive),透過馬達控制應變或剪切速率,即預設輸入為 φ 或 n,而上方偵測單元 (detector) 透過傳感器 (transducer) 測得 M (Fig. 11.6 圖右)。於雙頭系統,下方為轉子 (rotor),上方為定子 (stator),定子是靜止的或者可被偏轉極其有限的角度 (deflected to a very limited degree),偏轉的程度將取決於力矩傳感器 (torque transducer) 之剛性 (stiffness; 約 1 N/μm)。
Figures 11.7 和 11.8 分別為剪切應力控制 (shear stress-controlled) 和剪切速率控制 (shear rate-controlled) 模式流變儀的控制迴路 (control loops)。於 Fig. 11.7 的剪切應力控制迴路中,預設輸入 (input) 為 M or τ,電子控制器提供馬達一個適當的操作電流 I,使馬達產生對應的 M 於量測系統的樣品,造成偏轉角度 φ,並為位置感測器所記錄 (脈衝計數),最終輸出 (output) 為應變 γ 或剪切速率 γ_dot。因為摩擦總是存在,例如,軸承的摩擦阻力、運動中質量的慣性力 (包括旋轉夾具和樣品),這些擾動必需在實驗進行前透過電子控制器修正之。於 Fig. 11.8 的剪切速率控制迴路中,預設輸入 (input) 為 φ or γ,電子控制器也是同樣提供馬達一個適當的操作電流,使馬達產生對應的力矩 M 於量測系統的樣品,由位置感測器記錄實際的 (actual) 偏轉角度 φact。大部分的情況下,實際的 φact 將不同於輸入的 φ,所以經過電子控制器比對兩者的差異後,決定是否採用當下的力矩,如果差值過大,將進入一個封閉的控制迴路 (closed control loop),直到實際偏轉角度等於輸入偏轉角度,最終輸出 (output) 所需力矩或剪切應力。
 |
| Figure 11.7 剪切應力控制模式 (shear stress-controlled mode) |
 |
| Figure 11.8 剪切速率控制模式 (shear rate-controlled mode) |
最後討論一下軸承 (bearing),軸承用於連接旋轉軸 (rotation axis) 和靜止的機座 (stationary housing),有滾珠軸承 (ball bearing) 和空氣軸承 (air bearing) 兩種。我們必需特別注意的是,流變儀測得的總力矩 Mtot (total torque) 是以下各成份的相加
其中,M 來自於樣品的響應,應是總力矩 (Mtot) 的主要來源。Mf 來自於流變儀內部摩擦效應 (internal friction effects of the rheometer),如軸承阻力。Mi 來自於移動物質之慣性效應 (inertia effects),如旋轉夾具和樣品。流變儀經校準後 (adjustment),機械式的滾珠軸承之最小力矩值為 0.25 mNm 左右,而空氣軸承為 0.1 μNm 左右。兩者最小力矩解析約相差 1,000 倍。故現今空氣軸承的流變儀,可在使用單一夾具尺寸的情況下,量測範圍可以達到六個或更多的十進位 (six or more decades)。
Reference: TG Mezger, The Rheology Handbook, 3rd ed (Vincentz 2011).
化學流變學 (Chemorheology)
化學流變學 (chemorheology) 是描述交聯高分子 (cross-linking polymers) 於化學反應過程中 (例如,熟化 (curing) 或硫化 (vulcanization)) 之流變行為,最直接連想到的便是黏度的變化。流變量測能提供最直接的方法決定熟化和補捉凝膠點 (gel point)。
於反應射出成型 (reaction injection molding, RIM) 的充填 (filling) 過程中,我們必需知道黏度如何受各種變數之影響,因此,完整的黏度模型必需包括溫度 T、壓力 P、剪切率 γ_dot、熟化程度 c、填料性質 F 等效應,即
 (4)
(4)
如 Fig. 3.26 所示,當 G' = G" 時,稱之為凝膠點 ,所需時間為凝膠時間 (gel time);當 G' 變平緩且趨近一個常數,所需時間為熟化時間 (cure time)。Figure 3.27 是兩個不同升溫速率所對應的複數黏度 η* (complex viscosity) 和損耗正切 δ (loss tangent; tanδ = G"/G'),當升溫速率越高,凝膠點發生的時間越早。
於反應射出成型 (reaction injection molding, RIM) 的充填 (filling) 過程中,我們必需知道黏度如何受各種變數之影響,因此,完整的黏度模型必需包括溫度 T、壓力 P、剪切率 γ_dot、熟化程度 c、填料性質 F 等效應,即
以下我們簡單介紹 Castro-Macosko viscosity model,此模型同時考慮溫度、剪切率、熟化程度對黏度之影響,模型如下
我們的確可以注意到,Equation 2 包括了溫度對零剪切黏度的效應 η0(T)、剪切致稀的效應 (也就是 Cross model)、熟化對黏度的效應 (cg 為凝膠點的轉化率)。Figure 3.31 是環氧樹脂 (epoxy) 在不同溫度、轉化率下,其黏度對剪切率之作圖,這裡採用 Castro-Macosko 黏度模型。
 |
| Figure 3.31 Castro-Macosko 黏度模型 |
Figure 3.31 所使用的參數如下
這裡以溫度 T = 150℃、轉化率 c = 0.1、剪切率 γ_dot = 100 1/s 為例,計算該狀態下之黏度值。首先,溫度對零剪切黏度的效應為
接著,若再包括剪切率及轉化率的效應,黏度值變為
 (4)
(4)
以上是熟化反應對黏度的影響,接下來我們將簡短介紹熟化動力學 (curing kinetics) 的理論模型。常見的模型包括 n 階動力模型 (n-th order kinetic model)
和自催化動力模型 (autocatalytic kinetic model)
於 Eq. 6 中,生成物因自催化參與熟化反應,因此反應速率也與生成物濃度的 m 次方成正比 (即 cm)。由於實際的塑料配方複雜,因此,常見的做法便是結合以上兩種模型,成為組合型的模型如下 (combined kinetic model),即
由於射出成型是個非等溫的過程,因此我們必需考量反應常數是溫度的函數,簡單的數學表示式為
k1 = A1exp(-E1/RT) (8)
k2 = A2exp(-E2/RT) (9)
當進行模流計算時,隨著溫度與時間的演進,Equation 7 計算熟化反應速率,而 Eq. 2 計算黏度。
Reference:
1) T. Osswald and N. Rudolph, Polymer Rheology: Fundamentals and Applications (Hanser 2015).
2) 王茂齡、張榮語、許嘉翔,模流分析理論與實務 (科盛科技 Moldex3D 2018)。
2019年8月17日
Example 8.4-1: 小振幅振盪運動 (Small-Amplitude Oscillatory Motion))
於小振幅振盪剪切實驗中 (small-amplitude oscillatory shear experiment),剪切率的表示式為
其中,ω 是角頻率。我們知道積分型式的馬克斯威爾模型 (Maxwell model) 為 (張量表示式)
接著將 Eq. 8.4-10 的流場代入 Eq. 8.4-9 可得 (這裡僅使用 yx 分量)
其中,s = t - t'。我們知道於小振幅振盪運動,應力表示式為
若將 Eq. 8.4-11 與 Eq. 8.2-4 相比,我們可得複數黏度 η*(ω) (= η'(ω) - iη"(ω)),其實部 (動態黏度 η') 與虛部分別為
若將 Maxwell model 的鬆弛模數 G(t) (= Gexp (-t/λ)) 代入上式並積分可得
Equations 8.4-14 和 8.4-15 預測 η'(ω) 和 η"(ω) 均隨 ω 增加而變小,僅與實驗曲線定性吻合。此外,因 η' = G"/ω 和 η" = G'/ω,故儲存模數 G' 和損耗模數 G" 可表示為
Reference:
RB Bird, WE Stewart, EN Lightfoot, Transport Phenomena, 2nd ed
(Wiley 2002).
2019年8月16日
壓力體積溫度圖: Tait 方程式 (PVT Diagram: Tait Equation)
Revised: 2022/3/10
塑料的 pvT 圖可透過 pvT 設備測得,一般常用 Tait 方程式描述比容的實驗數據,即
其中,C = 0.0894。透過改變兩組 v0(T)、B(T)、vt(T, p) 常數,Tait 方程式可分別描述液態和固態兩區間的比容,其大致的溫度分水嶺為轉換溫度 Tt(p)
其中
隨壓力上升而增加的轉換溫度 Tt(p) 為Table 2.3 匯整 PC、PP、PS 樹脂的 Tait 方程式常數,實驗常用的降溫速率為 5 ℃/s (cooling rate)。有了材料對應的常數後,我們便可透過 Tait 方程式推算任何溫度、壓力之比容 (內插及外插)。Figure 2.14 是不定形高分子 PC 的 pvT 圖,轉換溫度發生於玻璃轉化溫度 Tg;Figure 2.16 是半結晶高分子 PP 的 pvT 圖,轉換溫度發生於熔點 Tm,也就是開始結晶的溫度。比較 Figs. 2.14 和 2.16,半結晶高分子因結晶形成局部規則排列,故其比容變化於降溫過程較無定形高分子來得急遽。
 |
| Table 2.3 各種高分子對應的 Tait 方程式常數值 |
 |
| Figure 2.14 PC 的 pvT 圖 |
 |
| Figure 2.16 PP 的 pvT 圖 |
Reference: TA Osswald, JP Hernandez-Ortiz, Polymer Processing: Modeling and Simulation (Hanser 2006).
動態機械分析之扭力試驗 (Dynamical Mechanical Analysis: Torsion Test)
扭力試驗 (torsion test) 經常於旋轉流變儀 (rotational rheometer) 上進行,然而,當進行扭力試驗時,我們需在流變儀上更換成專屬的扭力夾具 (fixture) 配件。樣品的幾何形狀主要有兩種,一種為細長的圓柱 (slender cylinder; Fig. 1 右圖) 或棒狀 (rod),另一種為矩形條 (rectangular bar; Fig. 2)。當碰到下述情況時,我們傾向使用扭力夾具而不是常見的雙平行板夾具 (parallel plates) 或錐平板夾具 (cone-and-plate geometry)。(i) 低溫時,樣品接近固態狀,易發生壁滑現象 (wall slip);(ii) 雙平行板的直徑過大,造成力矩 (torque) 超過儀器上限;(iii) 轉換器力移比 (transducer compliance) 過大。
 |
| Figure 1 圓柱狀試片 |
 |
| Figure 2 矩形條試片 |
我們先假定一個圓盤樣品 (disk-shaped sample) 如 Fig. 1 圖左,一般而言,我們需透過幾何常數 (geometry constants) 連結材料參數 (material parameters;應變 γ 與應力 σ) 與流變儀響應 (rheometer response;旋轉角度 θ 與力矩 M) ,即材料參數 = 儀器參數 × 幾何常數,應變幾何常數 Kγ 與應力幾何常數 Kσ 分別如下
其中,R 是圓盤的半徑、h 是樣品的厚度。如果圓盤樣品延伸成棒狀 (rod) 如 Fig. 1 圖右,此時,厚度 h 變成圓柱的長度 l,扭轉 D (twist) 可定義成
D = θ / l (3)
對圓柱或棒狀材料,其剪切模數 G 與扭轉度 D 和力矩 M 的關係為
其中,Jt 是極慣性矩 (polar moment of inertia)。因此,由 Eq. 3 可知,若需求得模數 G,我們需知道樣品 (或夾具) 的尺寸、旋轉角度、力矩。基本上,當扭轉度很小時,材料仍在線性區間,則使用扭力夾具和使用雙平行板夾具 (剪切實驗) 非常相似,即應力的分佈隨半徑由內向外呈線性增加 (Fig. 1 圖左上角或 Fig. 3a) 且對稱於中心軸,因此,無需對 Eq. 3 進行任何修正,便可得到正確的模數值。
 |
| Figure 3 應力分佈曲線 |
然而,對於矩形條的材料,情況較為複雜。如 Figs. 2 和 3b 所示,應力的分佈呈非線性,且等應力線 (stress contour) 並沒有對稱於中心旋轉軸。為此,De Saint Venant 針對試樣幾何 (specimen geometry),即寬度與厚度的比值 u (= w/t; width-to-thickness aspect ratio),提出剪切模數的修正如下
欲了解針對矩形條樣品的另一個修正,也就是,夾具效應 (clamping effect),請參考下方文獻 [Dessi et al. (2016)]。簡單來說,因為樣品的兩端是被夾具緊緊夾住的,這種夾擠效應會抑制試片的翹曲 (warp),且造成樣品扭力剛性 (torsional stiffness) 增加,因此實際測到的剪切模數會較大。為了修正這個效應,計算時必需使用修正後的樣品長度 (較短) 而不是實際的樣品長度 (較長)。
Reference:
1. A Frank, "Evaluation of the Correct Modulus in Rectangular Torsion," (TA Instruments).
2. C Dessi, GD Tsibidis, D Vlassopoulos, MD Corato, M Trofa, G D'Avino, PL Maffettone, and S Coppola, "Analysis of dynamic mechanical response in torsion," J Rheol 60, 275 (2016).
訂閱:
意見 (Atom)


































