一個固體材料 (solid material) 占有自 y = 0 到 y = ∞ 的空間,並在一開始時維持溫度 T0。當 t = 0,在 y = 0 位置的表面忽然被升溫至溫度 T1,並於 t > 0 之後,維持在該溫度。這是一個非穩態熱傳導的問題,試求時間相依的溫度曲線 T(y, t) (time-dependent temperature profiles)。
解答
對於固體,當上式結合傅立葉熱傳導定律 (Fourier's law of heat conduction) 則變成
如果熱傳導率 (thermal conductivity) 可以被假設與溫度和位置無關,則 Eq. 12.1-1 變成
其中,α 為固體的熱擴散率 (thermal diffusivity)。對於加熱一個半無限平板的問題 (heating a semi-infinite slab),Eq. 12.1-2 變成
這裡,我們介紹一個無因次的溫度差 Θ = (T - T0)/(T1 - T0),而初始和邊界條件為 (initial and boundary conditions)
I.C.: at t ≤ 0, Θ = 0 for all y (12.1-4)
B.C. 1: at y = 0, Θ = 1 for all t > 0 (12.1-5)
B.C. 2: at y = ∞, Θ = 0 for all t > 0 (12.1-6)
求解後得到
或
溫度曲線的結果繪於 Fig. 1。當 x 軸的 y/(4αt)0.5 ≈ 2,誤差函數 (error function) erf(y/(4αt)0.5) ≈ 0.99,(T - T0)/(T1 - T0) ≈ 0.01。所以,當 y 方向的熱穿透厚度 δT 為 (thermal penetration thickness)
也就是說,當 y > δT ,溫度的改變量將少於溫差 T1 - T0 的百分之一 (1%)。因此,若我們已知 α 的值 (高分子約為 10-7 m2/s),則可透過 Eq. 11 估算時間為 t 時,熱量傳遞的距離 。請注意,如果 δT 小於平板厚度 (slab thickness),則 Eq. 12.1-8 是很好的近似解;但是,如果 δT 相當於或大於平板厚度,則必需使用 Example 12.1-2 的級數解 (series solution)。
壁的熱通量 (wall heat flux) 可由 Eq. 10 計算之,即
因此,壁的熱通量隨 t-1/2 而變 (qy|y=0~t-1/2),而熱穿透厚度則隨 t1/2 而變 (δT~t1/2)。
 |
| Figure 1 |
Reference: RB Bird, WE Stewart, EN Lightfoot, Transport Phenomena, 2nd ed (Wiley 2002).





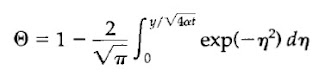



沒有留言:
張貼留言