這種流場是單一方向的 (unidirectional),也就是說僅有一個不為零的速度分量,因此,對於不可壓縮流體 (incompressible fluid),連續方程式 (continuity equation) 變成
Reference: T Osswald, JP Hernandez-Ortiz, Polymer Processing: Modeling and Simulation (Hanser 2006).
Equation 1 說明流體在 z 方向的流速,不隨 z 而改變。對於不可壓縮的牛頓流體,密度和黏度為定值,運動方程式 (equation of motion) 可簡化成 Navier-Stokes 方程式,其 z 方向的動量平衡方程式變成
而運動方程式的 x 和 y 分量則變成
Equation 3 指出,對於完全發展的流場,總壓力 (total pressure) 僅為 z 的函數。再者,因為速度向量 u (= uzδz) 不隨 z 而改變,壓力梯度 ¶p/¶z (= dp/dz) 必需是常數,所以
Equation 2 的動量方程式因此可寫成
當兩個無壁滑邊界條件 (two no-slip conditions) 被用於這個問題,即 uz(±h/2) = 0,積分兩次並利用這兩個邊界條件決定兩個積分常數後,可得速度函數
值得一提的是,當上述任一無壁滑邊界條件 (uz(+h/2) = 0 或 uz(-h/2) = 0) 被對稱條件 (symmetry condition) 取代 (y = 0,duz/dy = 0),仍可得到相同的速度分佈曲線。通道內的平均流體速度可從上式的積分得到,即
故可知,最大流速為平均速度的 1.5 倍。體積流率 Q 為
其中,W 為通道的寬度。Reference: T Osswald, JP Hernandez-Ortiz, Polymer Processing: Modeling and Simulation (Hanser 2006).





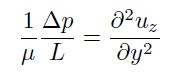



沒有留言:
張貼留言